In short:
I have implemented a simple (multi-key) hash table with buckets (containing several elements) that exactly fit a cacheline. Inserting into a cacheline bucket is very simple, and the critical part of the main loop.
I have implemented three versions that produce the same outcome and should behave the same.
The mystery
However, I'm seeing wild performance differences by a surprisingly large factor 3, despite all versions having the exact same cacheline access pattern and resulting in identical hash table data.
The best implementation insert_ok suffers around a factor 3 slow down compared to insert_bad & insert_alt on my CPU (i7-7700HQ). One variant insert_bad is a simple modification of insert_ok that adds an extra unnecessary linear search within the cacheline to find the position to write to (which it already knows) and does not suffer this x3 slow down.
The exact same executable shows insert_ok a factor 1.6 faster compared to insert_bad & insert_alt on other CPUs (AMD 5950X (Zen 3), Intel i7-11800H (Tiger Lake)).
# see https://github.com/cr-marcstevens/hashtable_mystery
$ ./test.sh
model name : Intel(R) Core(TM) i7-7700HQ CPU @ 2.80GHz
==============================
CXX=g CXXFLAGS=-std=c 11 -O2 -march=native -falign-functions=64
tablesize: 117440512 elements: 67108864 loadfactor=0.571429
- test insert_ok : 11200ms
- test insert_bad: 3164ms
(outcome identical to insert_ok: true)
- test insert_alt: 3366ms
(outcome identical to insert_ok: true)
tablesize: 117440813 elements: 67108864 loadfactor=0.571427
- test insert_ok : 10840ms
- test insert_bad: 3301ms
(outcome identical to insert_ok: true)
- test insert_alt: 3579ms
(outcome identical to insert_ok: true)
The Code
// insert element in hash_table
inline void insert_ok(uint64_t k)
{
// compute target bucket
uint64_t b = mod(k);
// bounded linear search for first non-full bucket
for (size_t c = 0; c < 1024; c)
{
bucket_t& B = table_ok[b];
// if bucket non-full then store element and return
if (B.size != bucket_size)
{
B.keys[B.size] = k;
B.values[B.size] = 1;
B.size;
table_count;
return;
}
// increase b w/ wrap around
if ( b == table_size)
b = 0;
}
}
// equivalent to insert_ok
// but uses a stupid linear search to store the element at the target position
inline void insert_bad(uint64_t k)
{
// compute target bucket
uint64_t b = mod(k);
// bounded linear search for first non-full bucket
for (size_t c = 0; c < 1024; c)
{
bucket_t& B = table_bad[b];
// if bucket non-full then store element and return
if (B.size != bucket_size)
{
for (size_t i = 0; i < bucket_size; i)
{
if (i == B.size)
{
B.keys[i] = k;
B.values[i] = 1;
B.size;
table_count;
return;
}
}
}
// increase b w/ wrap around
if ( b == table_size)
b = 0;
}
}
// instead of using bucket_t.size, empty elements are marked by special empty_key value
// a bucket is filled first to last, so bucket is full if last element key != empty_key
uint64_t empty_key = ~uint64_t(0);
inline void insert_alt(uint64_t k)
{
// compute target bucket
uint64_t b = mod(k);
// bounded linear search for first non-full bucket
for (size_t c = 0; c < 1024; c)
{
bucket_t& B = table_alt[b];
// if bucket non-full then store element and return
if (B.keys[bucket_size-1] == empty_key)
{
for (size_t i = 0; i < bucket_size; i)
{
if (B.keys[i] == empty_key)
{
B.keys[i] = k;
B.values[i] = 1;
table_count;
return;
}
}
}
// increase b w/ wrap around
if ( b == table_size)
b = 0;
}
}
My analysis
I've tried various modifications to the loop C , but inherently it's so simple, the compiler will produce the same assembly. It's really not obvious from the resulting assembly what the factor 3 loss might cause. I've tried measuring with perf, but I can't seem to pinpoint any meaningful difference.
Comparing the assembly of the 3 versions which are all just relatively small loops, there is nothing that suggests anything close that may cause a factor 3 loss between these versions.
Hence, I presume the 3x slow down is a weird effect of automatic prefetching, or branch prediction, or instruction/jump alignment or maybe a combination of those.
Does anybody have better insights or ways to measure what effects might actually be at play here?
Details
I've created a small working C 11 example that demonstrates the problem.
The code is available at 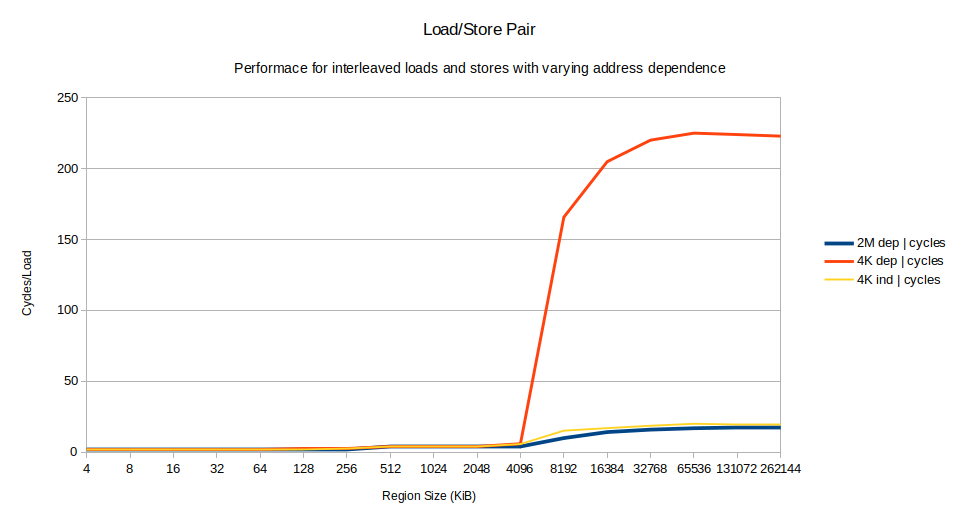
The performance of all the variants is basically identical for small region sizes. Everything up to 256 KiB takes 2 cycles/iteration, limited simply by the 8 uops in the loop and the 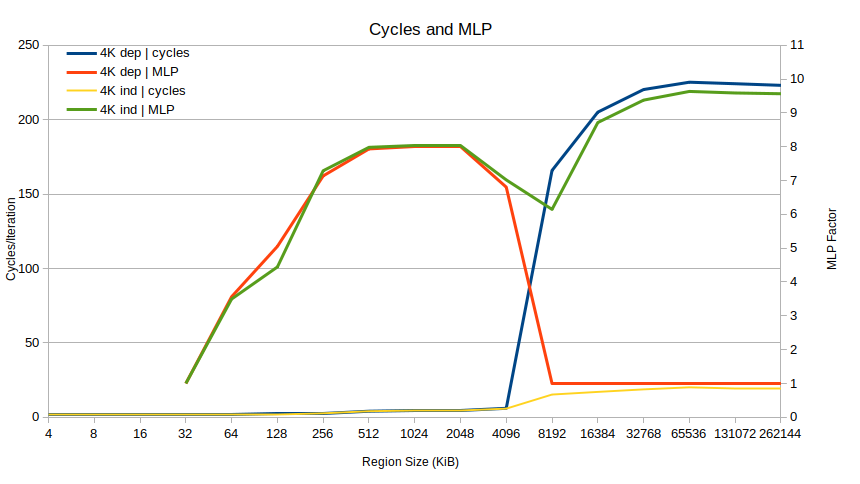
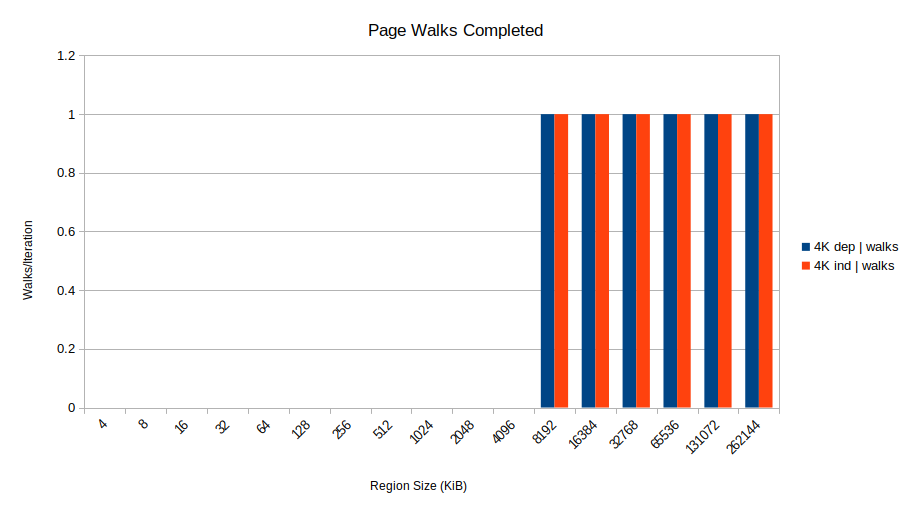
The problem becomes very clear. Up to regions of 4096 KiB, performance is identical, and MLP is high (for very small region sizes there is "no" MLP since there are no L1D misses at all). Suddenly at 8192 KiB, the MLP for the dependent case drops to 1 and stays there, while in the independent case the MLP goes to almost 10. That alone basically explains the 10x performance difference: the dependent case is not able to overlap loads, at all.
Why? The problem seems to be TLB misses. What happens at 8192 KiB is that the benchmark starts missing the TLB. Specifically, each Skylake core has 1536 STLB (second-level TLB) entries which can cover 1536 × 4096 = 6 MiB of 4K pages. So right between the 4 and 8 MiB region sizes, TLB misses go to 1 per iteration based on dtlb_load_misses.walk_completed, leading to this almost-too-perfect-is-it-take plot:
So that's what happens: when address-unknown stores are in the store buffer, loads that take STLB misses can't overlap: they go one-at-a-time. So you suffer the full memory latency for every access. This also explains why the 2MB page case was fast: 2 MB pages can cover 3 GiB of memory, so there are no STLB misses/page walks for these region sizes.
Why
This behavior seems to stem from the fact that Skylake and other earlier Intel processors implement page table coherence, even though the x86 platform does not require it. Page table coherence means that if a store which modifies an address mapping (for example) a subsequent load that uses a virtual address affected by the remapping will consistently see the new mapping without any explicit flushes.
This insight comes from Henry Wong who reports in his 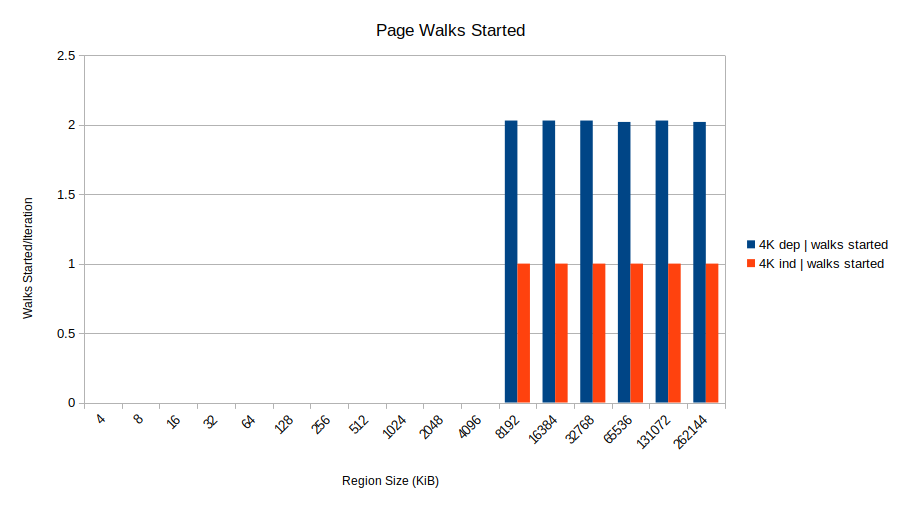
Huh! The 4K dependent shows two started walks, only one of which completes successfully. That's two walks for every load. This aligns with the theory that the page walk starts for the load in iteration N 1, but it finds the store from iteration N still sitting in the store buffer (since the load for iteration N provides its address, and it is still in progress). Since the address is unknown, the page walk is canceled as Henry describes. Further page walks are delayed until the store address is resolved. The upshot is all the loads complete in a serialized fashion because the page walk for load N 1 must wait for the result of load N.
Why the "bad" and "alt" methods are fast
Finally, there is one remaining mystery. The above explains why the original hash access was slow, but not why the other two were fast. The key is that both of the fast methods don't have address-unknown stores, because the data dependency with the load is replaced by a speculative control dependency.
Take a look at the inner loop for the insert_bad approach:
for (size_t i = 0; i < bucket_size; i)
{
if (i == B.size)
{
B.keys[i] = k;
B.values[i] = 1;
B.size;
table_count;
return;
}
}
Note that the stores use the loop index i. Unlike the insert_ok case, where the index [B.size] comes from a store, i is a simply a calculated value in a register. Now i is related to the loaded value B.size since its final value will be equal to it, but that is established via a comparison which is a speculated control dependency. It doesn't cause any problem with page walk cancellation. This scenario does have a lot of mis-predictons (since the loop exit is unpredictable) but for the large region case these aren't actually too harmful because the bad path usually makes the same memory accesses as the good path (specifically, the next value inserted is always the same) and memory access behavior dominates.
The same is true for the alt case: the index to write at is established by using a calculated value i to load a value, check if it is the special marker value and then writing at that location using index i. Again, no delayed store address, just a quickly calculated register value and a speculated control dependency.
What About Other Hardware
Like the question author, I found the effect on Skylake, but I also observed the same behavior on Haswell. On Ice Lake, I can't reproduce: both the dep and indep have almost identical performance. However user Noah reported he could reproduce on Tigerlake using the original benchmark. More investigation needed.
Run It Yourself
You can run the benchmark I describe above yourself. It's part of uarch-bench. On Linux (or WSL, but performance counters aren't available) you can run the following command to collect the results:
for s in 2M-dep 4K-dep 4K-indep; do ./uarch-bench --timer=perf --test-name="studies/memory/tlb-fencing/*$s" --extra-events=dtlb_load_misses.miss_causes_a_walk#walk_s,dtlb_load_misses.walk_completed#walk_c,l1d_pend_miss.pending#l1d_p,l1d_pend_miss.pending_cycles#l1d_pc; done
Some systems may not have enough free performance counters available (if you have hyperthreading enabled), so you can do two runs using different sets of counters each time.
1 In this case, rdx is always zero (the region is entirely full of zeros) so the store address happens to be the same as if this register wasn't included in the addressing expression, but the CPU doesn't know that!
2 Here, the 2M dep case also starts to show better performance than the 4K indep case, although the gap is modest.
3 Note the "while any miss is outstanding" part: you could also calculate MLP as l1d_pend_miss.pending / cycles, which would be the average MLP over a period of time, regardless of whether any misses were outstanding. Each is useful in their own way, but in a case like this with misses constantly outstanding they give almost identical values.
4 Yes, there are many differences between this and the original example. We store to a single fixed location, whereas the original loop stored near the load location, which varies every iteration. We store 0 not 1. We don't check B.size to see if it is too large. In our test the loaded value is always 0. There is no search loop for when the bucket is full. We don't load a random value to address, but just do a linear stride. However, these are not material: the same effect occurs in both cases and you can incrementally modify the original example by removing complexity until you reach this simple case.