Does the formula argument of geom_smooth mirror whats in aes()?-CodePudding

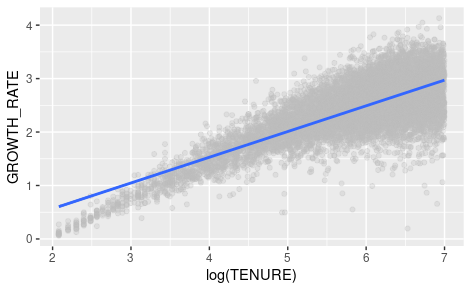
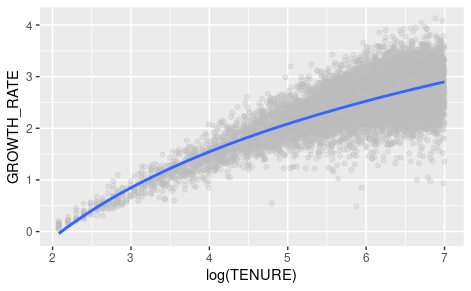
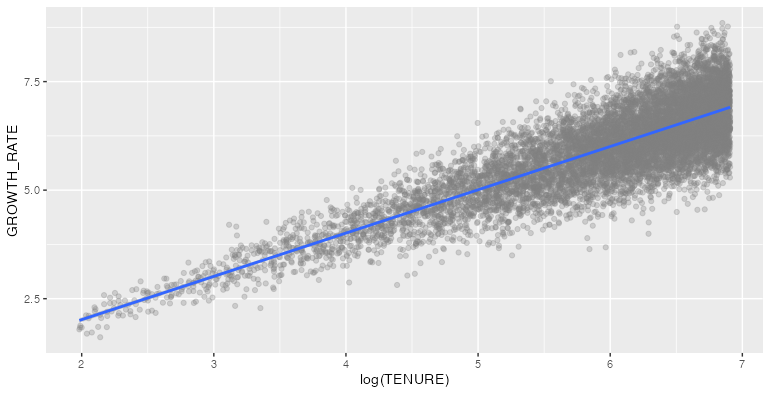
I have a ggplot for a logarithmic relationship between variable growth_rate and tenure:

pdata %>% 
  ggplot(aes(x = log(TENURE), y = GROWTH_RATE))  
  geom_point(color = 'gray', alpha = 0.3)  
  geom_smooth(method = 'lm', formula = 'y ~ x')

But the geom_smooth appears to fit better with:

pdata %>% 
  ggplot(aes(x = log(TENURE), y = GROWTH_RATE))  
  geom_point(color = 'gray', alpha = 0.3)  
  geom_smooth(method = 'lm', formula = 'y ~ log(x)')

Which plot is correct? Which plot shows a smooth fit line based on a linear model with formula y ~ log(TENURE)?

CodePudding user response：

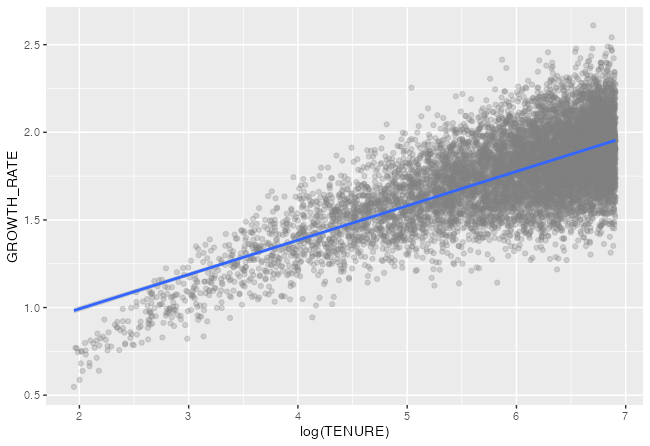
It looks like your underlying growth rate varies with the log of the log of tenure. Here's some sample data with that "log of log" relationship:

tibble(TENURE = runif(1E4, min = 7, max = 1000),
       GROWTH_RATE = rnorm(1E4, mean = 1, sd = 0.1) * log(log(TENURE))) %>%
  ggplot(aes(log(TENURE), GROWTH_RATE))  
  geom_point(alpha = 0.3, color = "gray50")  
  geom_smooth(method = 'lm', formula = 'y ~ x')

Plotting growth against the log results in a loose fit like your first one. Note that the lm is using the transformed values from your x and y mapping, so we can see that it is using log(TENURE) for x. (See bottom for a confirmation of that.)

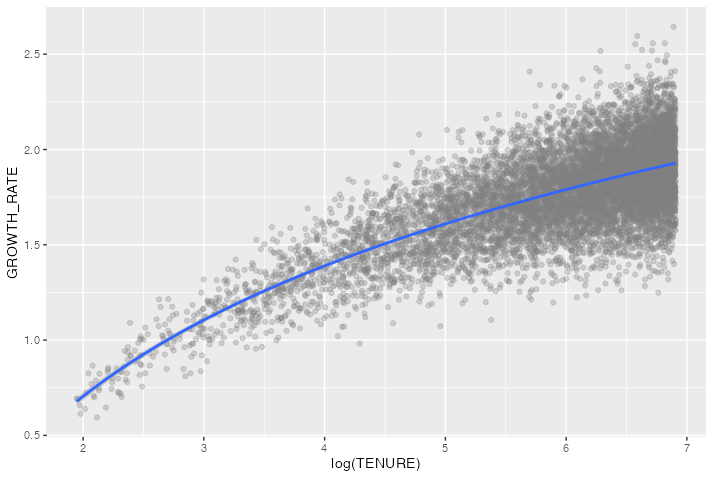
But modeling against the log of the log of tenure is a better fit. Here, when we use y ~ log(x), it means y ~ log( [log(TENURE)] ) since x is globally mapped in ggplot(aes(...)) to relate to the log of TENURE.

 ...   geom_smooth(method = 'lm', formula = 'y ~ log(x)')

If instead the original relationship had been a good fit for y ~ log(x), like the different generated data here, your first lm would have matched better:

tibble(TENURE = runif(1E4, min = 7, max = 1000),
       GROWTH_RATE = rnorm(1E4, mean = 1, sd = 0.1) * log(TENURE)) %>%
  ggplot(aes(log(TENURE), GROWTH_RATE))  
  geom_point(alpha = 0.3, color = "gray50")  
  geom_smooth(method = 'lm', formula = 'y ~ x')