Plotting Dose Response Curve from Survival Data-CodePudding

I would like to make a dose response curve from the library(drc), and am stuck on how to prepare my dataset properly in order to make the plot. In particular, I’m struggling how to get my y-axis ready.

I made up a dataframe (df) to help clarify what I would like to do.

df <- read.table("https://pastebin.com/raw/TZdjp2JX", header=T)

Open necessary libraries for today's exercise

library(drc)

library(ggplot2)

Let’s pretend I like humming birds, and do an experiment with different concentrations of sugar with the goal of seeing which concentration is ideal for humming birds. I therefore run an experiment in a closed setting (here column “room”), with 4 different sugar concentrations (column concentration), and 10 individual birds per concentration. I also run each experiment with 4 replicates in parallel, which is why there are 4 “rooms”. After 36 hours (column “time”), I go into the room, and check how many birds survived, creating a “yes/no” variable, or 1 & 0 (here, this is my column “status), where 1==survive, 0==died.

With this dataset, I specifically made it that most survived at concentration 0, 50% survived concentration 1, 25% survived concentration 2, and only 10% survive concentration 3.

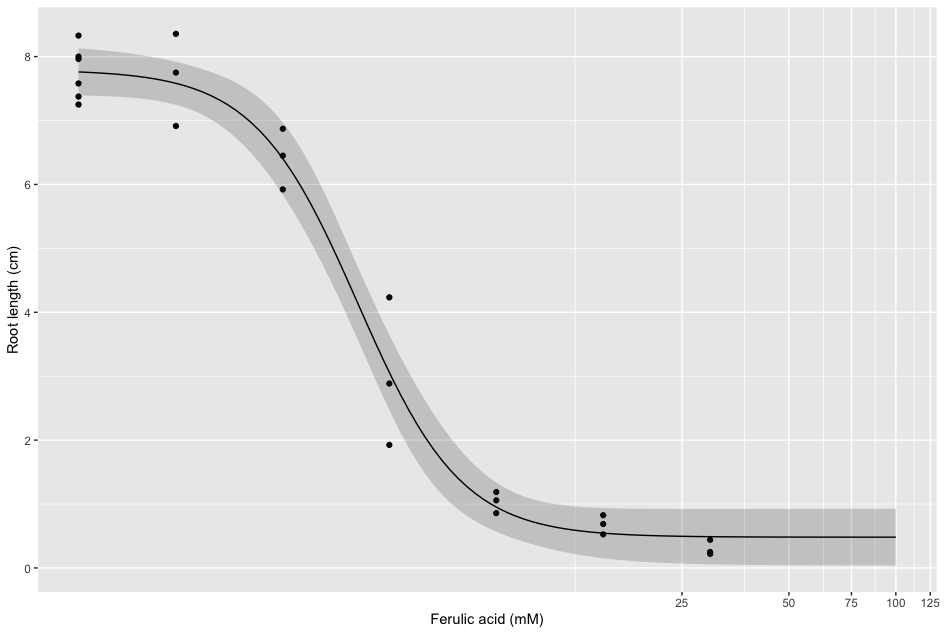
My first issue I’m running into is : how can I turn my y-axis , generated from my “status” column into a percentage? I have done this when I do kaplan-meier survival curves, but that does not work here unfortunately. Obviously, this should column should go from 0% - 100% (we could call the column "mortality"). After I succeed at doing this, I would like to make a dose response curve that looks like the following (I found this example online, and will directly copy it here to use an example. It is from the ryegrass dataset included in R)

ryegrass.LL.4 <- drm(rootl ~ conc, data = ryegrass, fct = LL.3())

I must admit, the next steps of code are a little confusing for me.

# new dose levels as support for the line
newdata <- expand.grid(conc=exp(seq(log(0.5), log(100), length=100)))
# predictions and confidence intervals
pm <- predict(ryegrass.LL.4, newdata=newdata, interval="confidence")
# new data with predictions
newdata$p <- pm[,1]
newdata$pmin <- pm[,2]
newdata$pmax <- pm[,3]

# plot curve

# need to shift conc == 0 a bit up, otherwise there are problems with coord_trans
ryegrass$conc0 <- ryegrass$conc
ryegrass$conc0[ryegrass$conc0 == 0] <- 0.5
# plotting the curve
ggplot(ryegrass, aes(x = conc0, y = rootl))  
  geom_point()  
  geom_ribbon(data=newdata, aes(x=conc, y=p, ymin=pmin, ymax=pmax), alpha=0.2)  
  geom_line(data=newdata, aes(x=conc, y=p))  
  coord_trans(x="log")  
  xlab("Ferulic acid (mM)")   ylab("Root length (cm)")

In the end, I would like to generate a similar curve, but with mortality on the y-axis, from 0-100 (starting low, going high) and also display the confidence intervals in a shaded grey area around the regression line. Meaning, my first step of code should like something like the following:

model <- drc(mortality ~ Concentration, data=df, fct = LL.3()) But I'm lost on the "mortality" creation part, and a little bit on the next step with ggplot

Could anyone help me achieve this? From the example from ryegrass, I'm perplexed how to translate this to be helpful for my pretend dataset. I hope someone here is able to help me solve this issue! Many thanks, and I appreciate any feedback if there are other ways I should have my dataset structured, etc.

-Andy

CodePudding user response：

library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union
library(ggplot2)
library(drc)
#> Loading required package: MASS
#> 
#> Attaching package: 'MASS'
#> The following object is masked from 'package:dplyr':
#> 
#>     select
#> 
#> 'drc' has been loaded.
#> Please cite R and 'drc' if used for a publication,
#> for references type 'citation()' and 'citation('drc')'.
#> 
#> Attaching package: 'drc'
#> The following objects are masked from 'package:stats':
#> 
#>     gaussian, getInitial

df <- read.table("https://pastebin.com/raw/sH5hCr2J", header=T)

Making the mortality or as I do here survival, can be done easily with the dplyr package. This will help perform many calculations. It seems that you are interested in calcuating the percent survival for each Concentration across your four rooms (or replicates). So the first step is to group the data by these columns and then calculate the statistic we want.

df_calc <- df %>%
  group_by(Concentration, room) %>%
  summarise(surv = sum(Status)/n())
#> `summarise()` has grouped output by 'Concentration'. You can override using the `.groups` argument.

I don’t know if Concentration represents arbitrary Concentration levels so I’m moving forward with the following assumption:

1 == higher levels of sugar, 2 == lower levels of sugar
Concentrations were coding in log space - so I convert to linear space

df_calc <- mutate(df_calc, conc = exp(-Concentration))

Just to be clear, the conc variable is just my attempt at having something close to the true known concentrations of the experiment. If your data has the true concentrations, then don't mind this calculation.

df_calc
#> # A tibble: 12 x 4
#> # Groups:   Concentration [3]
#>    Concentration  room  surv   conc
#>            <int> <int> <dbl>  <dbl>
#>  1             1     1   0.5 0.368 
#>  2             1     2   0.4 0.368 
#>  3             1     3   0.5 0.368 
#>  4             1     4   0.6 0.368 
#>  5             2     1   0   0.135 
#>  6             2     2   0.4 0.135 
#>  7             2     3   0.2 0.135 
#>  8             2     4   0.4 0.135 
#>  9             3     1   0.2 0.0498
#> 10             3     2   0   0.0498
#> 11             3     3   0   0.0498
#> 12             3     4   0.2 0.0498

mod <- drm(surv ~ conc, data =  df_calc, fct = LL.3())

Make new conc data points

newdata <- data.frame(conc = exp(seq(log(0.01), log(10), length = 100)))

Use the model and the generated data points to predict a new surv value as well as the upper and lower bound

newdata <- cbind(newdata,
                 suppressWarnings(predict(mod, newdata = newdata, interval="confidence")))

plot with ggplot2

ggplot(df_calc, aes(conc))  
  geom_point(aes(y = surv))  
  geom_ribbon(aes(ymin = Lower, ymax = Upper), data = newdata, alpha = 0.2)  
  geom_line(aes(y = Prediction), data = newdata)  
  scale_x_log10()  
  coord_cartesian(ylim = c(0, 1))

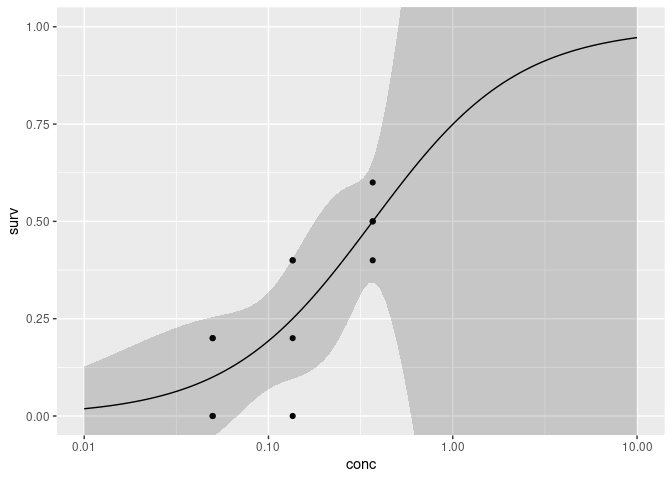
As you may notice, the confidence intervals increase greately when we try and predict ranges that has no data.

^{Created on 2021-10-27 by the reprex package (v1.0.0)}