I'm trying to implement an AVL tree as a practice. For both insertion and deletion operations, my implementation does the normal BST insertion and deletion first, and then walks up the parent chain to check and fix any unbalanced subtrees. However, I'm not sure how to decide between the zig-zig and zig-zag case when the child of the unbalanced node has a balance factor of 0. I thought I could choose either one in this case, but this doesn't work for deletion.

Suppose the tree looks like this and I want to remove 78,

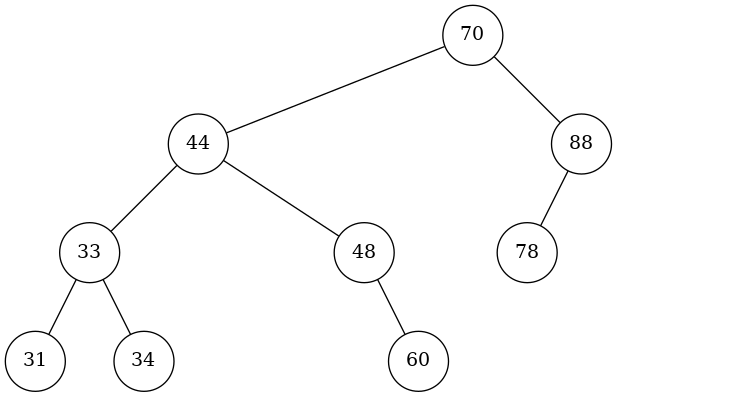
The rebalancing method would walk up to 70 (the root), find it unbalanced, then here comes the problem: because 44 has a balance factor of 0, should I perform the Zig-zig case on 70-44-33, or the Zig-zag case on 70-44-48 ?

The latter would fail to balance the tree. Left Rotation around 44 followed by Right Rotation around 70 would produce the following result: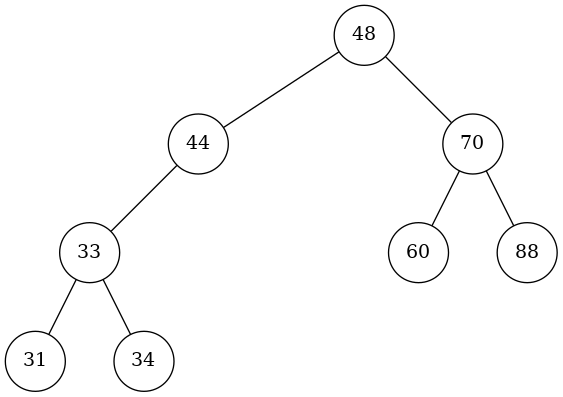

On the other hand, the zig-zig case (Right Rotation around 70) is the right way to go: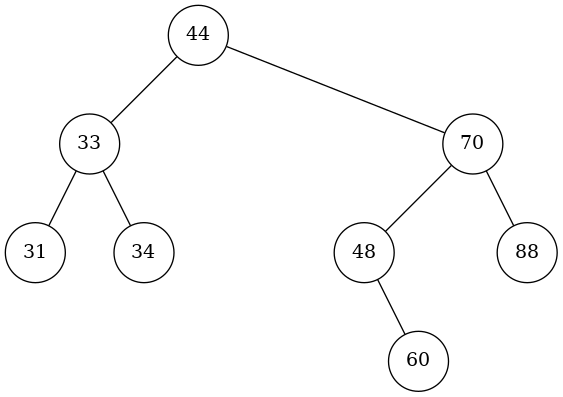

CodePudding user response：

It is unusual to use the "zig zag" terminology with AVL trees. That terminology is more common for Splay trees (also balancing trees), where the purpose is to bubble a particular node to the top through rotations. There is no such purpose in AVL trees. The terminology for AVL trees consists of simple rotations (from left to right or vice versa) and double rotations (combinations of two simple rotations).

When after a deletion of a node you move upwards in the tree, and find a balance-violation, this means that the temporarily updated balance factor in that node is either -2 or 2.

If the child on the heavy side has a balance factor that has an opposite sign (so 1 when its unbalanced parent has -2; or -1 when its unbalanced parent has 2), then a double rotation is needed. In all other cases a simple rotation is needed.

The case of the inner heavy grandchild, which requires a double rotation, is depicted here (copied from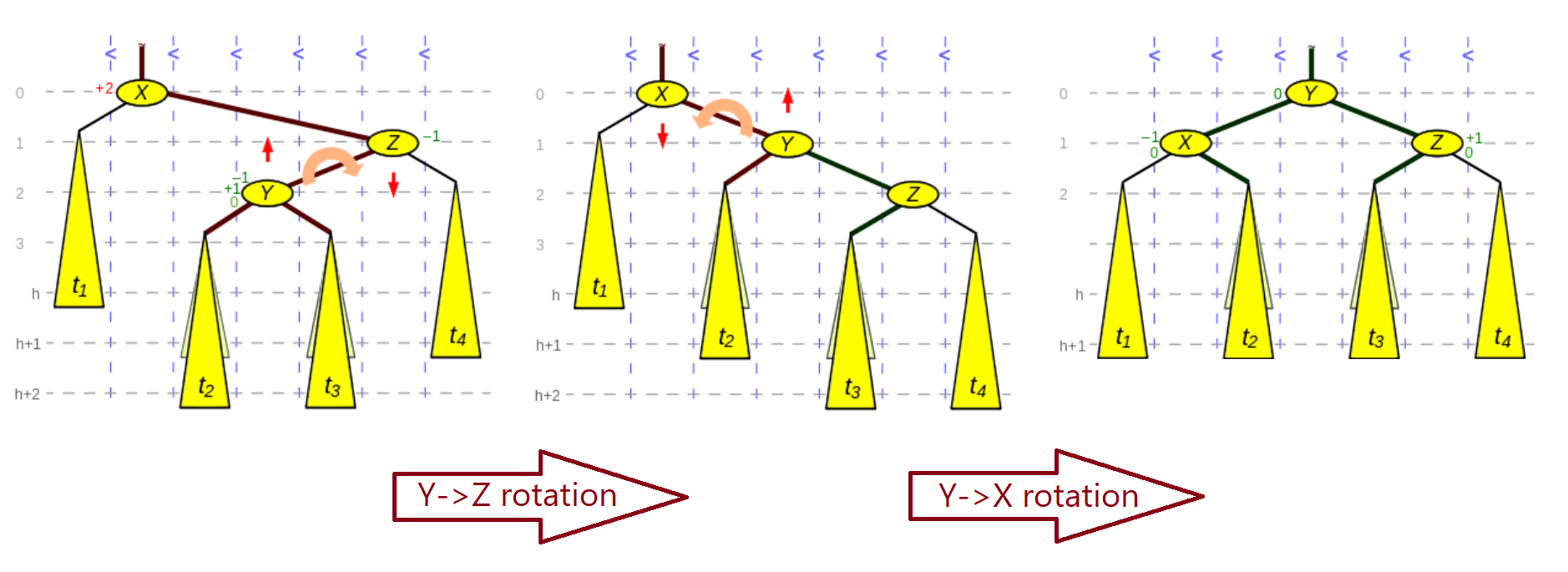

In your example the node 44 has balance factor 0, so no double rotation is needed, and you should just rotate the root from left to right. If we imagine the same tree, but without nodes 31 and 34 (making 33 a leaf), then the balance factor at 44 would be 1 (opposite sign to the -2 at 70) and a double rotation would have been needed.