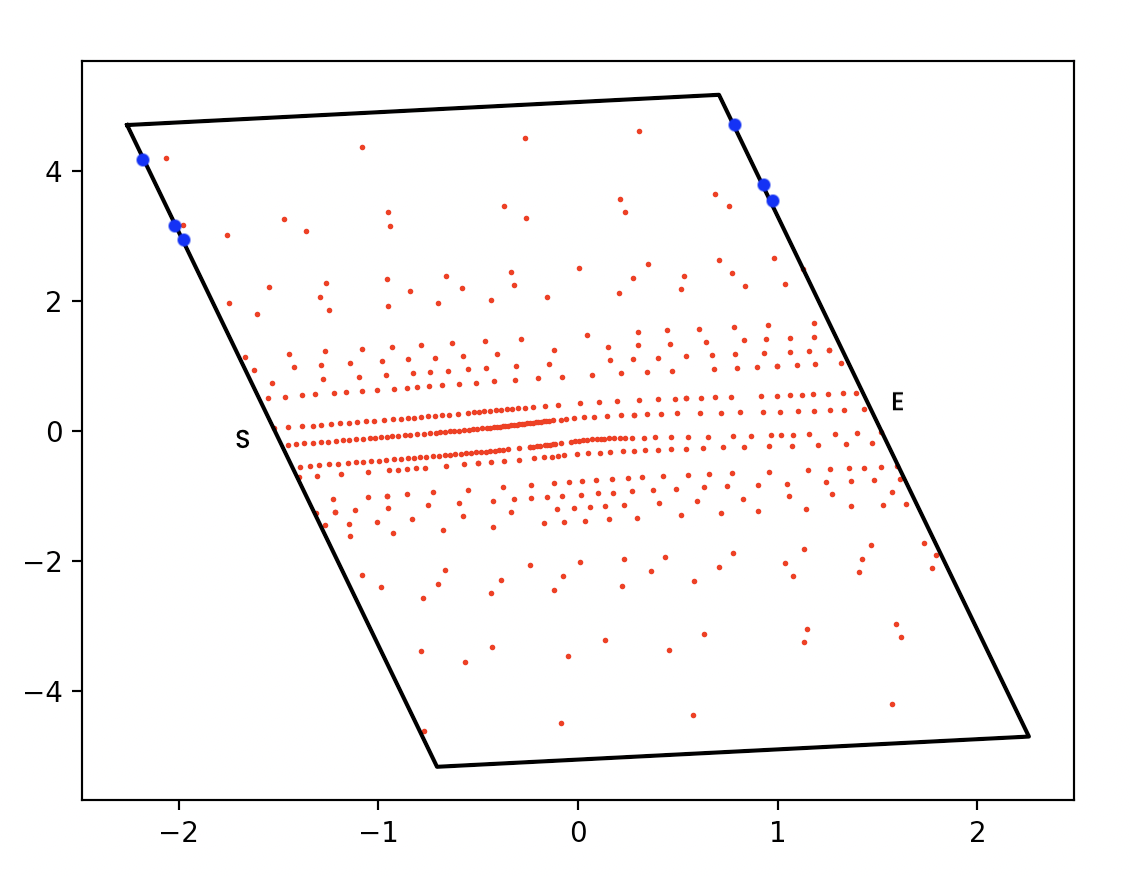
I have a set of lines made of points of which I have to compute the total distance from the section S to the section E.

To do that I am computing the sum of the euclidean distances of the consecutive points of each line, however, some lines are less dense of points than the others. In particular, to compute the real total distance of every line I need that the first and last point of each one lie respectively on the section S and E. To do that I was thinking of adding "fake points" on the sections (the ones colored in blue) without distorting the direction of the lines which are generally parallel to the upper and lower sections of the bounding box.

I have the coordinates of the vertices of the bounding box and the angular coefficient of the segments that compose it.

How can I compute the coordinates of the fake points?

CodePudding user response：

Perhaps use linear regression to find the slope and intercept of the three "lines" of points, then solve a system of equations with two unknowns to get the intersection of each line with the bounding box.