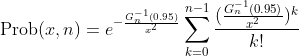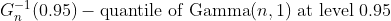How to deal with very big numbers producing NaN-CodePudding

I want to define very simple function following:

where:

My work so far

prob <- function(x, n) {
  quan <- qgamma(0.95, n, 1)
  temp <- quan / (x)^2
  first_term <- exp(-temp)
  second_term <- temp^(0:(n - 1)) / factorial(0:(n - 1))
  second_term <- sum(second_term)
  first_term * second_term
}

The problem here is that in the sum (second term) for big n we are dealing with very big numbers, so R treats those as infinity.

So for example:

prob(0.5, n = 1000)
[1] NaN

Because quantile for n = 1000 equals to 1052.577, in nominator we have to calculate 1052.577^999 and in denominator factorial of 999. R understands those two numbers as infinity:

> factorial(999)
[1] Inf
> 1052.577^999
[1] Inf

So when it tries to divide them NaN is produced. However the output of this function is always in interval (0, 1), since its a probability. Is there any possibility to calculate value of this function in this point?

CodePudding user response：

Your prob function is just the cumulative Poisson with lambda = temp and k = n - 1. Use ppois:

prob <- function(x, n) {
  return(ppois(n - 1, qgamma(0.95, n, 1)/x^2))
}

prob(0.5, n = 1000)
# [1] 0

prob(0.5, n = 1000) = 0 because n - 1 = 999 is so far from the mean (lambda = qgamma(0.95, 1000, 1)/0.5^2 = 4210.308).