Trouble plotting a rotated right triangle in matplot-CodePudding

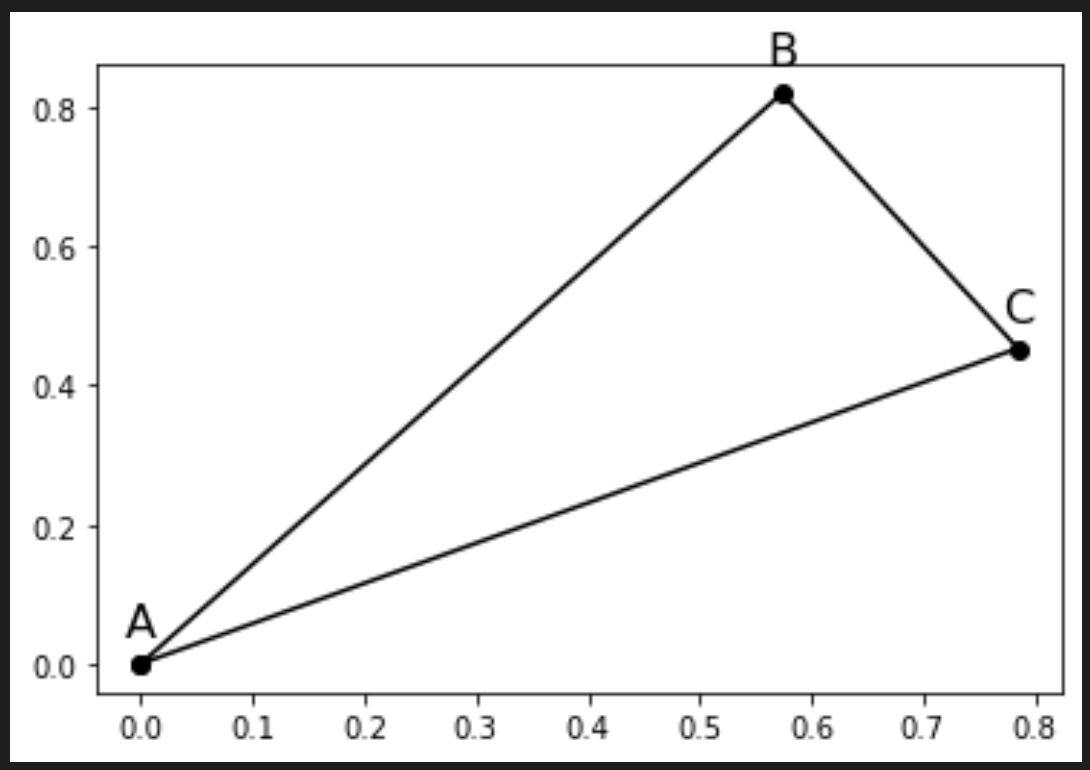
I'm trying to generate a right triangle with hypotenuse = 1, interior angle 25, that is rotated 30 degrees. I've entered the trig formulas correctly to my understanding, and I suspect some kind of rounding error. Because the triangle produced in matplot is slightly off from a right triangle.

import math
import matplotlib.pyplot as plt
from annotation import label

angle_b = math.radians(25) # the interior 25 degree angle of our right triangle
angle_a = math.radians(30) # 30 degree angle between the plotted angle_b triangle and the x axis.

point_A = (0,0)
point_B = (math.cos(angle_a   angle_b), math.sin(angle_a   angle_b))
point_C = (math.cos(angle_a) * math.cos(angle_b), math.sin(angle_a) * math.cos(angle_b))

# Label our points
label(plt, 'A', point_A)
label(plt, 'B', point_B)
label(plt, 'C', point_C)

# Draw the right triangle between our points.
plt.plot(*zip(point_A, point_B, point_C, point_A), marker='o', color='black')

As you can see, the angle ACB is not a right angle as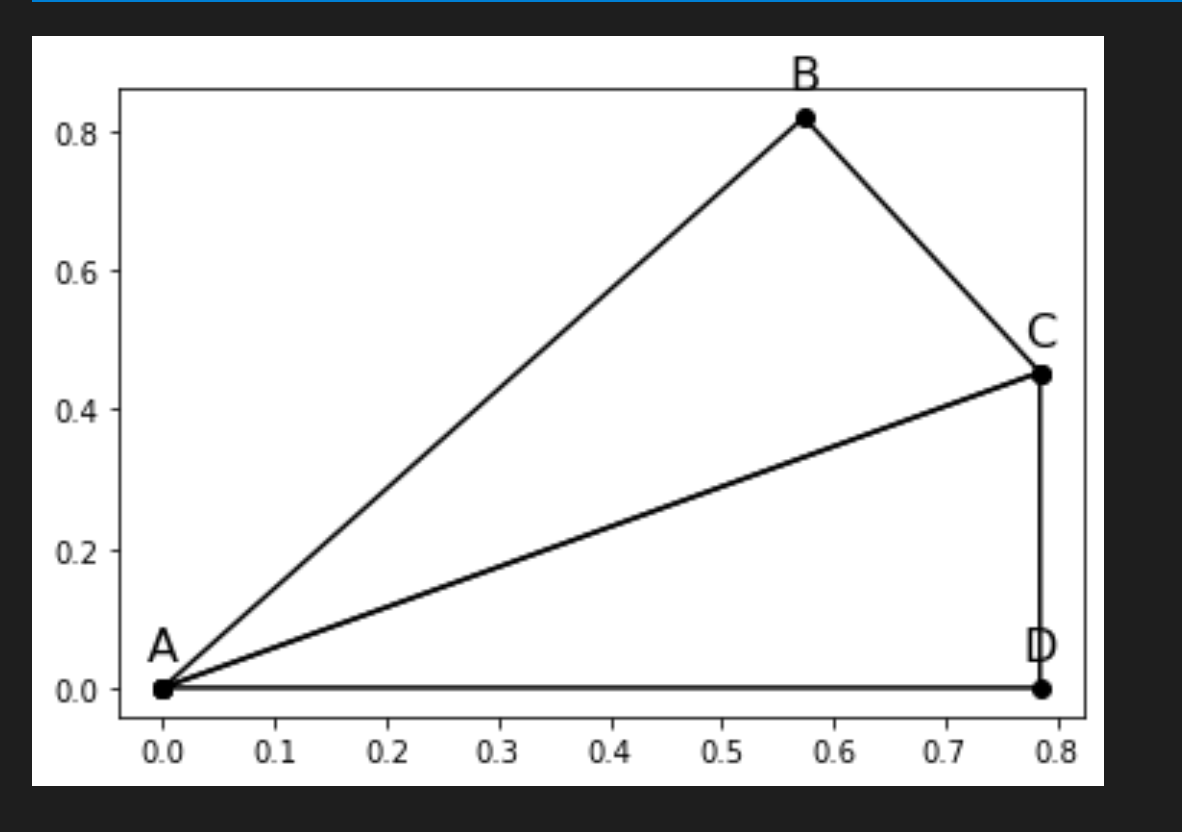

CodePudding user response：

You appear to have jumbled your trigonometry. I'm going to suggest moving slowly step-by-step, and using variable names that help you remember what is going on.

Let's start with the original triangle. If interior_angle = np.deg2rad(25) and the hypotenuse has length 1, then the right angle on the x-axis is at (np.cos(interior_angle), 0) and the other interior angle is at (np.cos(interior_angle), np.sin(interior_angle)). Neither of the points in your diagram corresponds.

Now let's express the triangle as a matrix whose columns are the vertices:

interior_angle = np.deg2rad(25)
vertices = np.array([
    [0, np.cos(interior_angle), np.cos(interior_angle), 0],
    [0, 0, np.sin(interior_angle), 0],
])

The last vertex is a repeat of the origin to make plotting easier.

Now let's look at the rotation. For rotation_angle = np.deg2rad(30), point (x, y) rotates to (np.cos(rotation_angle) * x - np.sin(rotation_angle) * y, np.sin(rotation_angle) * x np.cos(rotation_angle) * y). This can be expressed as a matrix equation:

rotation_matrix = np.array([
    [np.cos(rotation_angle), -np.sin(rotation_angle)],
    [np.sin(rotation_angle), np.cos(rotation_angle)]])
p_out = rotation_matrix @ p_in

The array vertices is so constructed that it can be directly multiplied by a rotation matrix. You can therefore write

rotation_angle = np.deg2rad(30)
rotation_matrix = np.array([
    [np.cos(rotation_angle), -np.sin(rotation_angle)],
    [np.sin(rotation_angle), np.cos(rotation_angle)]])
rotated_vertices = rotation_matrix @ vertices

The plotted image should make more sense now:

plt.plot(*vertices)
plt.plot(*rotated_vertices)

CodePudding user response：

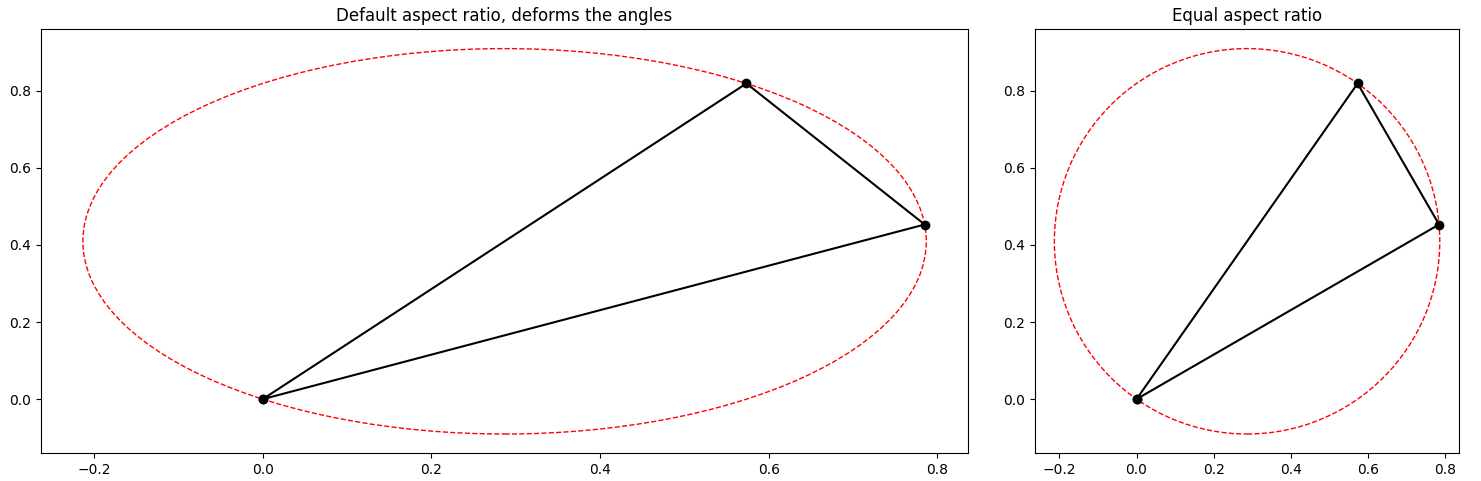
The problem is that by default, matplotlib doesn't use the same distances in the x and in the y direction. Instead, matplotlib tries to fit everything nicely into the given bounds.

These uneven distances distort angles, and also deforms circles.

You can force an equal aspect ratio via ax.set_aspect('equal').

import matplotlib.pyplot as plt
import math

angle_b = math.radians(25)  # the interior 25 degree angle of our right triangle
angle_a = math.radians(30)  # 30 degree angle between the plotted angle_b triangle and the x axis.

point_A = (0, 0)
point_B = (math.cos(angle_a   angle_b), math.sin(angle_a   angle_b))
point_C = (math.cos(angle_a) * math.cos(angle_b), math.sin(angle_a) * math.cos(angle_b))

point_M = ((point_A[0]   point_B[0]) / 2, (point_A[1]   point_B[1]) / 2)

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(16, 4), gridspec_kw={'width_ratios': [2, 1]})

for ax in (ax1, ax2):
    # Draw the right triangle between our points.
    ax.plot(*zip(point_A, point_B, point_C, point_A), marker='o', color='black')
    # draw a circle around the 3 points
    ax.add_patch(plt.Circle(point_M, math.sqrt((point_M[0] - point_A[0]) ** 2   (point_M[1] - point_A[1]) ** 2),
                            ec='r', ls='--', fc='none'))
ax1.set_title('Default aspect ratio, deforms the angles')
ax2.set_aspect('equal')  # or plt.axis('equal')
ax2.set_title('Equal aspect ratio')
plt.tight_layout()
plt.show()