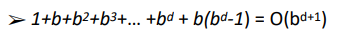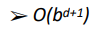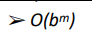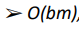I didn't understand these complexities of BFS and DFS for BFS it's written that time complexity is (d is the depth of the solution node in the tree and b is the maximum number of node sons)

the space complexity is written to be

for DFS time complexity is (m is the max depth of the tree)

and its space complexity is

Can someone please explain where these come from

CodePudding user response：

For BFS, every iteration you are exploring a queue of nodes, building the next queue and recursing into it.

def bfs(startNode, target):
  queue = [startNode]
  while len(queue) > 0:
    next_queue = []
    for node in queue:
      if node == target: return True
      next_queue.append(node.children)
    queue = next_queue
  return False

At first, the queue only has one element, but because every node in the queue has all its children added to the next queue, and because each node can have up to b children, the size of the queue can grow by a factor of b every iteration. You may have 1 node in the queue the first iteration then up to b nodes in the second loop, each of those b nodes may themselves add b nodes to the third queue, yielding b*b = b^2 nodes, then b^3 nodes the next loop, and so on. This can go on until the target node is reached at depth d, at which point there could be up to b^d nodes in the queue. Because the queue is being held in memory, this costs O(b^d) space, and because each node in the queue is processed in (presumably) constant time every iteration of the loop, the time complexity is as you stated O(1 b b^2... b^d) = O(b^{d 1}). (Note that this would still be O(b^m) if the target is not in the graph.)

On to dfs:

def dfs(node, target):
  if node == target: return True
  found = false
  for child of node.children:
    found = dfs(child, target)
    if found: break
  return found

For dfs, there is no guarantee that your search takes the right branch to go straight to the target node. You go as deep as possible, recursively exploring the first child of every node until the search bottoms out before you branch to the side. As such, you could search much deeper than the depth d of the target node and could, in the worst case, explore to the maximum depth and process the whole graph before the target is found. As the Graph can contain up to b^m nodes, dfs's time complexity is O(b^m). To analyze the space complexity, note that you could make up to m recursive calls before your search bottoms out. Making a function call takes space: a call stack of depth m requires at least O(m) space. However, each recursive call on a given node references all of that node's up to b children, requiring O(b) space. This means that each call on the call stack takes O(b) space, and as there are up to m such calls, O(bm) space can be required in total for dfs.