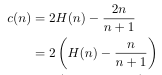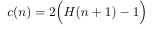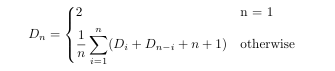For a research project I'm using the isolation forest algorithm. The developers of this algorithm make use of Binary Search Tree theory. They state that the average depth in an unsuccessful search in a Binary Search Tree (c(n)) is defined as:

c(n)=2H(n−1)−(2(n−1)/n)

where H(n-1) is the harmonic number and can be estimated by ln(n-1) 0.5772156649 (Euler's constant) and n is the number of terminal nodes in the tree.

Can somebody please explain (mathematically) where these formulas come from?

CodePudding user response：

Note that these formulas only apply for a tree whose keys were added in a random order with respect to their natural ordering: nothing is assumed about the shape or balance of the tree other than that which can be expected from a random insertion order (if we knew the tree was perfectly balanced the math would be different, and much simpler). They also assume that each unsuccessful search has an equal likelihood of terminating at any null pointer in the tree (as without any prior knowledge about the shape of the tree or the distribution of its values, any endpoint is equally likely).

I will note that the provided formula for the cost in terms of average depth is undefined for n=1 (it seems unnecessarily right-shifted by 1). I don't know the definitions for depth and cost that they're using, but it seems reasonable to say the average depth explored to for a singleton tree is 1, not undefined (as an unsuccessful search on that node will check either its empty left pointer or its empty right pointer before terminating, exploring to a depth of 1). I would shift their formula back to the left by 1 to accommodate this case as:

This formulation still slightly underestimates average depth (to a noticeable degree for n<~50) relative to the more simple formula I will be using (equivalent to the former one as n approaches infinity but more accurate for smaller n):

With that said, you can frame the average cost of an unsuccessful search in a random tree of n nodes, T, exactly in terms of the average depth of the null pointers in T (as each unsuccessful search terminates at some null pointer, with a cost proportional to that pointer's depth, and we assume all null endpoints are equally likely to be reached). To get the average null depth for T, it will be easier to get the total null depth, D, and divide by the number of null pointers.

Note that every tree of n nodes has n 1 null pointers. You can prove this with induction, with a tree of 1 node having 2 null pointers, and every new node you add to a tree replacing one null pointer but adding two more, preserving the invariant that there is 1 more null pointer than there are nodes. With this in mind, there's a recursive way to analyze the total null depth for any tree:

Base case: A tree with 1 node has a total null depth of 2.

Recursive case: A tree with n nodes can have it's null pointers laid out n different ways depending on which node is chosen to be the root: if the smallest node, n_1, is chosen as the root, there will be 0 nodes and thus 0 1 = 1 null ptrs in in the left subtree, and n-1 nodes and n null ptrs in the right subtree. If the n_2 is chosen as the root, there will be 1 node and 2 null pointers in the left subtree, and n-2 nodes with n-1 null pointers in the right, and so on, up until you have all nodes and all but 1 null pointers in the left subtree, and no nodes but 1 null pointer in the right subtree. Also, regardless of how you split the n 1 null pointers into left and right subtrees, all n 1 null pointers in those subtrees each have their depths increased by one because they all get put under the chosen root (which is where the " n 1" term comes from in the recurrence). Since the tree and therefore the choice of root to split on is random, all splits are equally likely, so you average across all n possible splits to get the expected total null pointer depth for a size n tree, D_n = c(n)(n 1) (you still have to divide the total null depth by the number of pointers to get the average search depth).

These cases are expressed mathematically in the recurrence:

Check the top answer to this similar question for why when you solve this recurrence and divide the result by n 1, the result is c(n) = 2(H(n 1) - 1) (just substitute m in their math with n 1, and t with D).

As for why the natural log approximates harmonic numbers, that's a separate question, but basically it boils down to the fact that H(x) = 1/1, 1/2, ... 1/x, and the integral of 1/x with respect to x is ln(x).

Here's an experiment showing the derived formula to be correct, using exact harmonic numbers and approximated ones:

import sys
import math
from random import random
from functools import cache

class TreeNode:
  def __init__(self, value):
    self.value = value
    self.left = None
    self.right = None

class BST:
  def __init__(self, values):
    self.root = None
    self.num_nodes = len(values)
    for value in values: 
      self.root = self.insert(value)

  def insert(self, value):
    def _insert(root, value):
      if not root: return TreeNode(value)
      if value < root.value:
        root.left = _insert(root.left, value)
      else:
        root.right = _insert(root.right, value)
      return root
    return _insert(self.root, value)
  
  # total depth of all None pointers
  def total_external_depth(self):
    if not self.root: return None
    total = 0
    def traverse(root, depth = 0):
      nonlocal total
      if root is None: 
        total  = depth
        return
      traverse(root.left, depth 1)
      traverse(root.right, depth 1)
    traverse(self.root)
    return total
  
  # average depth of all None ptrs in tree
  def average_external_depth(self):
    if not self.root: return None
    return self.total_external_depth() / (self.num_nodes   1)

max_tree_size = 10
trials = 1000
if len(sys.argv) > 1: max_tree_size = int(sys.argv[1])
if len(sys.argv) > 2: trials = int(sys.argv[2])

results = [0] * max_tree_size

for tree_size in range(1, max_tree_size   1):
  for trial in range(trials):
    T = BST([random() for i in range(tree_size)])
    results[tree_size-1]  = T.average_external_depth()
  results[tree_size-1] /= trials

@cache # memoized harmonic numbers
def H(n):
  if n == 1: return 1
  return 1/n   H(n-1)

# approximate harmonic numbers
def _H(n): return math.log(n)   0.5772156649

for i, x in enumerate(results):
  n = i 1
  expt = results[i]
  derived = 2*(H(n 1) - 1)
  approx = 2*(_H(n 1) - 1)
  experimental_error = (expt - derived) / derived * 100
  approximation_error = (approx - derived) / derived * 100
  print('C({}):\texperimental: {:.3f}\tapprox: {:.3f}\tderived: {:.3f}'.format(i 1, expt, approx, derived))
  print('\terror: expt: {:.2f}{}\tapprox: {:.2f}{}'.format(experimental_error, '%', approximation_error, '%'))