I have a directed acyclic graph created by users, where each node (vertex) of the graph represents an operation to perform on some data. The outputs of a node depend on its inputs (obviously), and that input is provided by its parents. The outputs are then passed on to its children. Cycles are guaranteed to not be present, so can be ignored.

This graph works on the same principle as the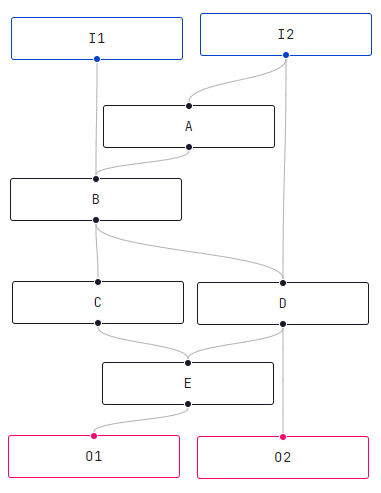

A traditional breadth-first traversal would result in D being evaluated prior to B, despite D depending on B.

I've tried doing a breadth-first traversal in reverse (that is, starting with the O1 and O2 nodes, and traversing up the graph), but I seem to run into the same problem. A reversed breadth-first traversal will visit D before B, thus I2 before A, resulting in I2 being ordered after A, despite A depending on I2.

I'm sure I'm missing something relatively simple here, and I feel as though the reverse traversal is key, but I can't seem to wrap my head around it and get all the pieces to fit. I suppose one potential solution is to use the reverse traversal as intended, but rather than avoiding visiting each node more than once, just visiting each node each time it comes up, ensuring that it has a definitely correct ordering. But visiting each node multiple times and the exponential scaling that comes with that is a very unattractive solution.

Is there a well-known efficient algorithm for this type of problem?

CodePudding user response：

Yes, there is a well known efficient algorithm. It's topological sorting.

Create a dictionary with all nodes and their corresponding in-degree, let's call it indegree_dic. in-degree is the number of parents/or incoming edges to that node. Have a set S of the nodes with in-degree equal to zero.

Taken from the Wikipedia page with some modification:

L ← Empty list that will contain the nodes sorted topologically
S ← Set of all nodes with no incoming edge that haven't been added to L yet

while S is not empty do
    remove a node n from S
    add n to L
    for each child node m of n do
        decrement m's indegree
        if indegree_dic[m] equals zero then
            delete m from indegree_dic
            insert m into S

if indegree_dic has length > 0 then
    return error   (graph is not a DAG)
else 
    return L   (a topologically sorted order)

This sort is not unique. I mention that because it has some impact on your algorithm.

Now, whenever a change happens to any of the nodes, you can safely avoid recalculation of any nodes that come before the changed node in your topologically sorted list, but need to nodes that come after it. You can be sure that all the parents are processed before their children if you follow the sorted list in your calculation.

This algorithm is not optimal, as there could be nodes after the changed node, that are not children of that node. Like in the following scenario:

    A
   /  \
  B    C

One correct topological sort would be [A, B, C]. Now, suppose B changes. You skip A because nothing has changed for it, but recalculate C because it comes after B. But you actually don't need to, because B has no effect on C whatsoever.

If the impact of this isn't big, you could use this algorithm and keep the implementation easier and less prone to bugs. But if efficiency is key, here are some ideas that may help:

1. You can do a topological sort each time and include the which node has change as a factor. When choosing nodes from S in the above algorithm, choose every other node that you can before you choose the changed node. In other words, you choose the changed node from S only when S has length 1. This guarantees that you process every node that isn't below the hierarchy of the changed node before it. This approach helps when the sorting is much cheaper then processing the nodes.

2. Another approach, which I'm not entirely sure is correct, is to look after the changed node in the topological sorted list and start processing only when you reach the first child of the changed node.

3. Another way relies on idea 1 but is helpful if you can do some pre-processing. You can create topological sorts for each case of one node being changed. When a node is changed, you try to put it in the ordering as late as possible. You save all these ordering in a node to ordering dictionary and based on which node has changed you choose that ordering.