Construct and describe an efficient algorithm which takes as input two directed acyclic graphs (DAG's) and finds the longest path which occurs in both of them.

If there are several, the algorithm should return one of the longest paths (it doesn't matter which one). In summary, given the graphs G = (V,E) and G' =(V',E'), find the longest possible sequence <v1,...,vk> where (v_i,v_{i 1}) is in E and E' for i = 1...k-1.

Any ideas? I can write the actual code myself, I just need help with building the idea behind the actual algorithm and finding a solution to the problem.

Im thinking I could use recursive DFS and some memoization: while keeping track of visited nodes; for each starting node and for each neighbour, calculating the distance to the neighbour the distance from the neighbour to the goal. Then taking the max of these, memoizing it as the max from this node, and returning it.

Using this approach for both DAG's, the issue from here would be to identify which of these paths is the longest that occurs in both.

Would appreciate any ideas/help.

CodePudding user response：

Two approaches:

1. Starting from every vertex, figure out what is the longest common path. DFS memoize. Return the max length. If you want the path as well, memoize the longest path as well.

2. Find the intersection of the DAGs and return the longest intersecting path. You can find

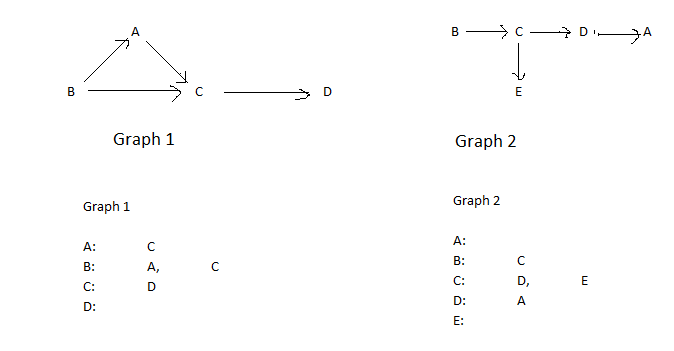
   In first approach, you find out length of maximum matching path (BCD here) and return the length.

   In second approach, you'll store the matching parts (BCD here) and return the longest path length from it.

   

   Approach 3:

   @"n. 1.8e9-where's-my-share m." mentions another approach in the comments where you delete the edges from one graph which are not present in another graph.

   So, if you delete from graph 1 the edges which are not present in graph 2, you'll get the below:

   

   In the above graph if you do the DFS, you'll get 3 as answer as BCD is the longest path.