How to fit Gaussian distribution with one-sided data?-CodePudding

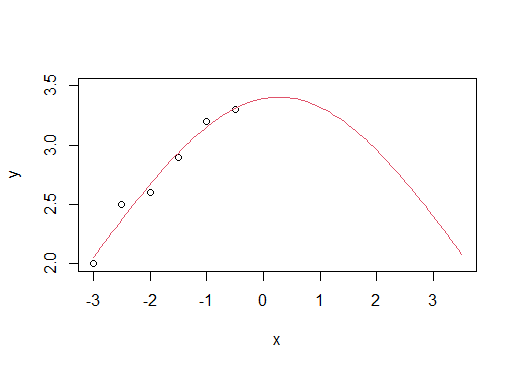
x <- c(-3,-2.5,-2,-1.5,-1,-0.5)
y <- c(2,2.5,2.6,2.9,3.2,3.3)

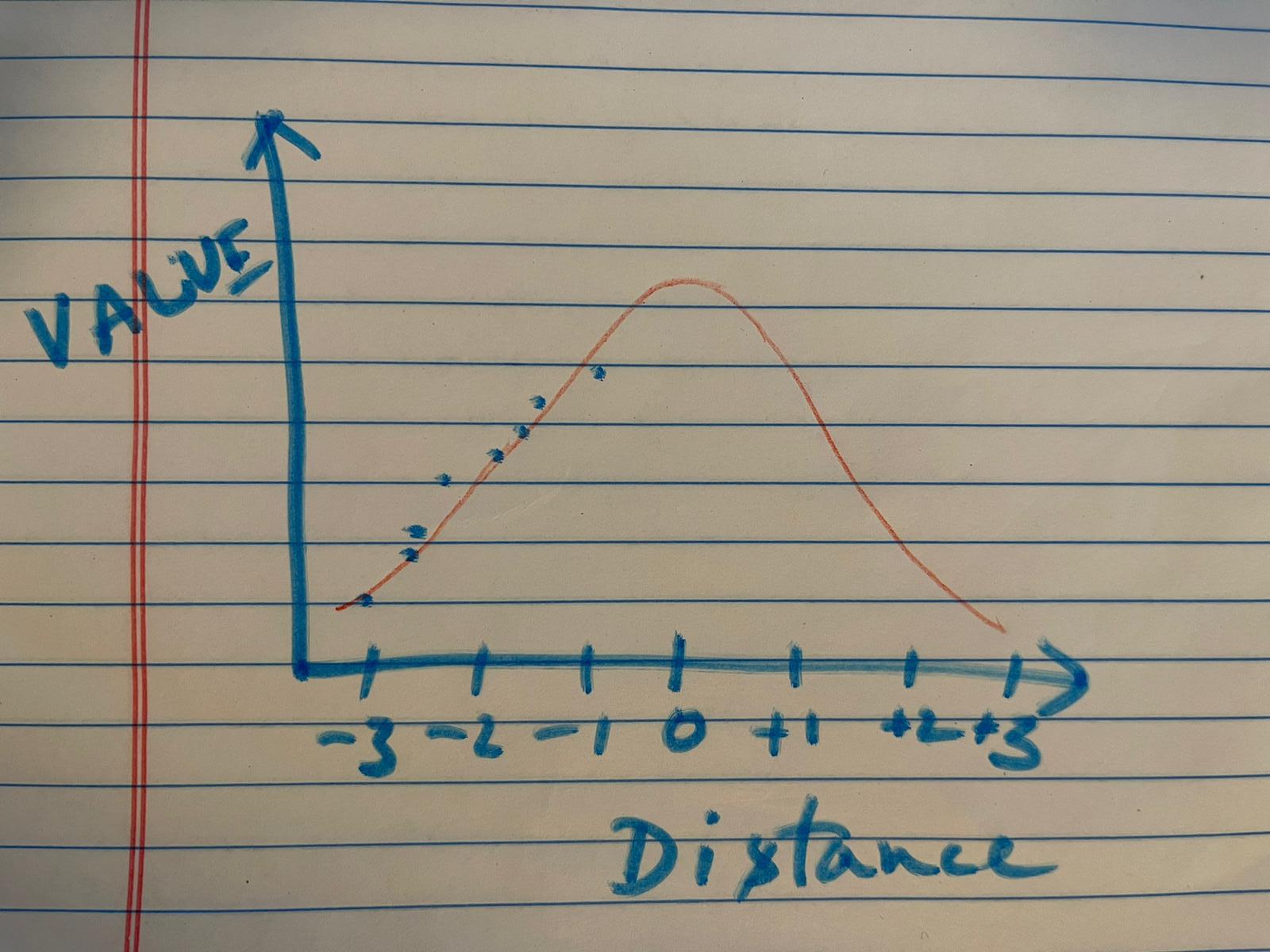
enter image description here

The challenge is that the entire data is from the left slope, how to generate a two-sided Gaussian Distribution?

CodePudding user response：

There is incomplete information with regards to the question. Hence several ways can be implemented. NOTE that the data is insufficient. ie trying fitting tis by nls does not work.

Here is one way to tackle it:

f <- function(par, x, y )sum((y - par[3]*dnorm(x,par[1],par[2]))^2)
a <- optim(c(0,  1, 1), f, x = x, y = y)$par
plot(x, y, xlim = c(-3,3.5), ylim = c(2, 3.5))
curve(dnorm(x, a[1], a[2])*a[3], add = TRUE, col = 2)

CodePudding user response：

There is no way to fit a Gaussian distribution with these densities. If correct y-values had been provided this would be one way of solving the problem:

# Define function to be optimized
f <- function(pars, x, y){
  mu <- pars[1]
  sigma <- pars[2]
  y_hat <- dnorm(x, mu, sigma)
  se <- (y - y_hat)^2
  sum(se)
}

# Define the data
x <- c(-3,-2.5,-2,-1.5,-1,-0.5)
y <- c(2,2.5,2.6,2.9,3.2,3.3)

# Find the best paramters
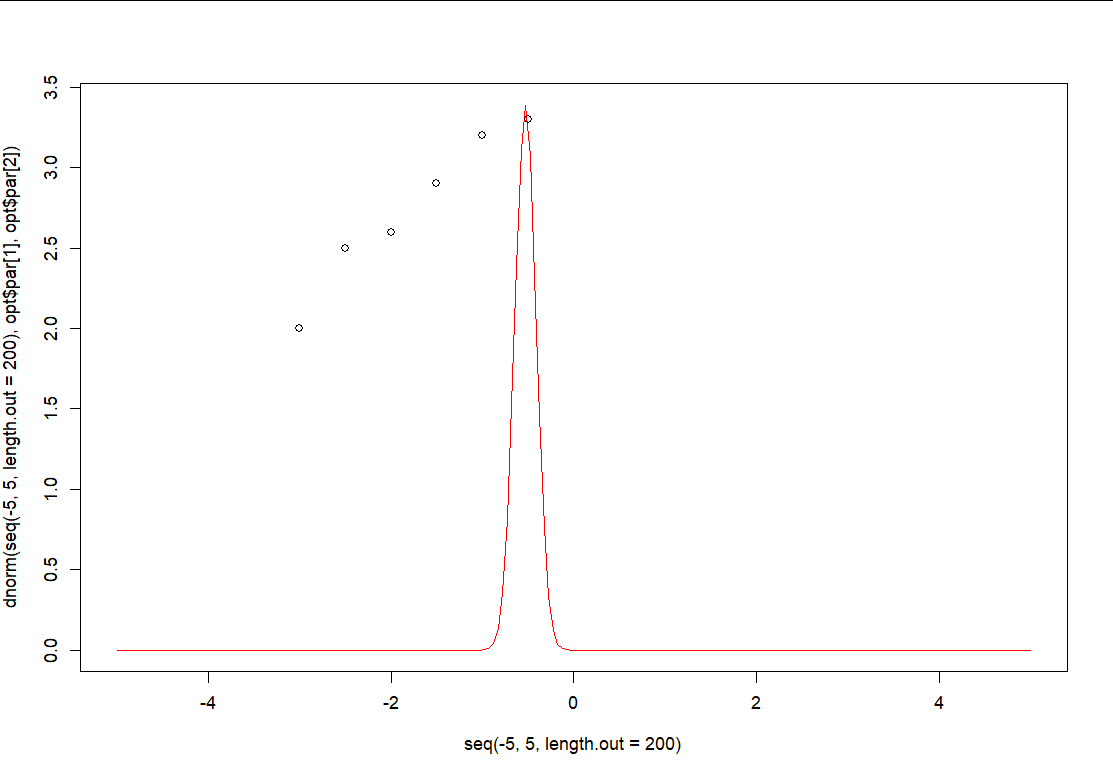
opt <- optim(c(-.5, .1), f, 'SANN', x = x, y = y)

plot(
  seq(-5, 5, length.out = 200),
  dnorm(seq(-5, 5, length.out = 200), opt$par[1], opt$par[2]), type = 'l', col = 'red'
)
points(c(-3,-2.5,-2,-1.5,-1,-0.5), c(2,2.5,2.6,2.9,3.2,3.3))