Here is the code with which I store the .txt file:
ifstream f("file.txt");
string str1;
if (f.is_open())
{
getline(f,str1);
while(f)
{
cout << str1 << endl;
getline(f, str1);
}
f.close();
}
}
The problem is, that the str1[i] access the i-th symbol of the whole dataset. I'd like to find all local maxima of the second column of the dataset. Here is the example of the dataset:
15497.97740 -0.174807
15497.99247 0.410084
15498.00754 0.680590
15498.02260 -0.887408
15498.03767 -1.383546
15498.05273 -0.741141
CodePudding user response:
One of the ways that you can do this is to load the second column into a vector and then find maximum element in that vector. You can read your file either by lines or by individual numbers using std::fstreams operator>>(double). The second approach seems simpler in this case.
Notice that you don't need to manually close the file since the file is closed automatically in std::fstreams destructor.
#include <algorithm>
#include <iostream>
#include <fstream>
#include <vector>
int main()
{
std::fstream ifs("data.txt");
if (!ifs.is_open())
{
return 1;
}
std::vector<double> secondColumn;
// read the file skipping the first column
double d1;
double d2;
while (ifs >> d1 && ifs >> d2)
{
secondColumn.push_back(d2);
}
// use the algorithm library to find the max element
// std::max_element returns end iterator if the vector is empty
// so an additional check is needed
auto maximumIt = std::max_element(secondColumn.begin(), secondColumn.end());
if (maximumIt != secondColumn.end())
{
double maximum = *maximumIt;
std::cout << maximum << '\n';
}
}
CodePudding user response:
I am sorry to say, but your question is not fully clear to me. Sorry for that.
Anyway, I will try to help. I will find ALL local maxima.
We will split down the big problems into small problems, with classes and methods. That is then easier to solve.
Let's start with the basic element. A point on a curve. We will create a mini class, containing an “x” and “y”, assuming that this is your column 1 and column 2. We will add very easy input end output functions.
// One point. Has a X and a Y coordinate. Can be easily read and written
struct Point {
// Data
double x{};
double y{};
// Ultra simple input and output function
friend std::istream& operator >> (std::istream& is, Point& p) { return is >> p.x >> p.y; }
friend std::ostream& operator << (std::ostream& os, const Point& p) { return os << std::setprecision(10) << p.x << " \t " << p.y; }
};
Next. This is a curve. It simply consists of many points. We will use a std::vector to store the Point elements, because the std::vector can grow dynamically. We will add also here very simple input and output functions. For the input, we read Points in a loop and add them to our internal std::vector. The output will simply write all values of our std::vector to the output stream “os”.
Next, reading the data from a file. Because we already defined the input and outpit operators for a Point and a Curve base on a stream, we can simply use the standard extractor << and inserter >> operators.
The first approach will then look like that:
int main() {
// Open the sourcefile with the curve data
std::ifstream sourceFileStream{"r:\\file.txt"};
// Check, if we could open the file
if (sourceFileStream) {
// Here, we will store our curve data
Curve curve{};
// Now read all all points and store them as a curve
sourceFileStream >> curve;
// Show debug output
std::cout << curve;
}
else std::cerr << "\n*** Error: Could not open source file\n";
}
Hm, looks really cool and simple. But, how does it work? First, we open the file with the constructor of the std::ifstream. That is easy. And the nice thing is, the destructor of the std::ifstream will close the file for us automatically. This happens on the next closing brace }.
Tio check, if the stream is still OK or has a failure, we can simply write if (sourceFileStream). This is possible, because the ``std::ifstream’s booloperator is overwritten. And since the if` statement expects a Boolean value, this operator is called and informs us, if there is a problem or not. True means no problem. Nice.
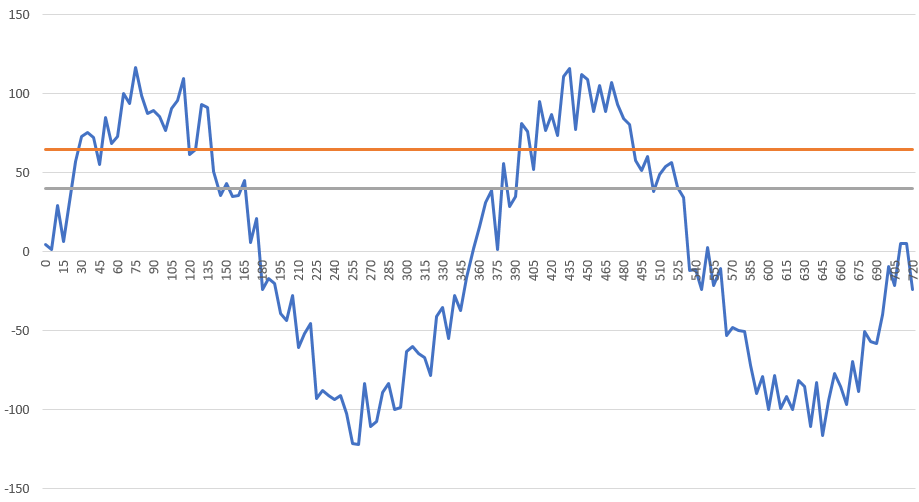
Now, lets come to the local peak value search. The problem is often a discrete signal with overlayed noise. Let us look at the following example with a base sinusoid curve and some heavy noise:
We will add 2 thresholds. An upper and a lower one, or just an upper one but with a negative hysteresis. Sounds complicated, but is not. First, we will check the absolute maximum and absolute minimum value of the curve. Based on that we will calculate the thresholds as percentage values.
We will evaluate value by value and if we pass the upper threshold, we will start looking for a maximum. We will do this until we cross the lower threshold. At this moment, we will store the so far calculated max value (together with its x value). Then, we wait until we cross again the upper threshold. The hysteresis will prevent continuous toggling of the search mode in case of noise.
All this put in code could look like that:
std::vector<Point> Curve::findPeaks() {
// Definition of Threshold value and hysteresis to find max peak values
constexpr double ThreshholdPercentageHigh{ 0.7 };
constexpr double Hyteresis{ 0.2 };
constexpr double ThreshholdPercentageLow{ ThreshholdPercentageHigh - Hyteresis };
// First find the overall min / max to calculate some threshold data
const auto [min, max] = std::minmax_element(points.cbegin(), points.cend(), [](const Point& p1, const Point& p2) { return p1.y < p2.y; });
const double thresholdMaxHigh = ((max->y - min->y) * ThreshholdPercentageHigh min->y);
const double thresholdMaxLow = ((max->y - min->y) * ThreshholdPercentageLow min->y);
// We need to know, if the search is active
// And we need to know, when there is a transition from active to inactive
bool searchActive{};
bool oldSearchActive{};
// Initiliaze with lowest possible value, so that any other value will be bigger
double maxPeakY{ std::numeric_limits<double>::min() };
// X value for the max peak value
double maxPeakX{ std::numeric_limits<double>::min() };
std::vector<Point> peaks{};
// Go through all values
for (size_t index{}; index < points.size(); index) {
// Check,if values are above threshold, then switch on search mode
if (not searchActive) {
if (points[index].y > thresholdMaxHigh)
searchActive = true;
}
else {
// Else, if value is lower than lower threshold, then switch of search mode formaxpeak
if (points[index].y < thresholdMaxLow)
searchActive = false;
}
// If the search is active, then find the max peak
if (searchActive)
if (points[index].y > maxPeakY) {
maxPeakX = points[index].x;
maxPeakY = points[index].y;
}
// Check for a transition from active to inactive. In that very moment, store the previosuly found values
if (not searchActive and oldSearchActive) {
peaks.push_back({ maxPeakX, maxPeakY });
maxPeakY = std::numeric_limits<double>::min();
}
// Remember for next round
oldSearchActive = searchActive;
searchActive = points[index].y > thresholdMaxHigh;
}
return peaks;
}
Leading to a final solution with everything put together:
#include <iostream>
#include <fstream>
#include <vector>
#include <iomanip>
#include <algorithm>
// One point. Has a X and a Y coordinate. Can be easily read and written
struct Point {
// Data
double x{};
double y{};
// Ultra simple input and output function
friend std::istream& operator >> (std::istream& is, Point& p) { return is >> p.x >> p.y; }
friend std::ostream& operator << (std::ostream& os, const Point& p) { return os << std::setprecision(10) << p.x << " \t " << p.y; }
};
// A curve consists of many pointes
struct Curve {
// Data
std::vector<Point> points{};
// find peaks
std::vector<Point> findPeaks();
// Ultra simple input and output function
friend std::istream& operator >> (std::istream& is, Curve& c) { Point p{}; c.points.clear(); while (is >> p) c.points.push_back(p); return is; }
friend std::ostream& operator << (std::ostream& os, const Curve& c) { for (const Point& p : c.points) os << p << '\n'; return os; }
};
std::vector<Point> Curve::findPeaks() {
// Definition of Threshold value and hysteresis to find max peak values
constexpr double ThreshholdPercentageHigh{ 0.7 };
constexpr double Hyteresis{ 0.2 };
constexpr double ThreshholdPercentageLow{ ThreshholdPercentageHigh - Hyteresis };
// First find the overall min / max to calculate some threshold data
const auto [min, max] = std::minmax_element(points.cbegin(), points.cend(), [](const Point& p1, const Point& p2) { return p1.y < p2.y; });
const double thresholdMaxHigh = ((max->y - min->y) * ThreshholdPercentageHigh min->y);
const double thresholdMaxLow = ((max->y - min->y) * ThreshholdPercentageLow min->y);
// We need to know, if the search is active
// And we need to know, when there is a transition from active to inactive
bool searchActive{};
bool oldSearchActive{};
// Initiliaze with lowest possible value, so that any other value will be bigger
double maxPeakY{ std::numeric_limits<double>::min() };
// X value for the max peak value
double maxPeakX{ std::numeric_limits<double>::min() };
std::vector<Point> peaks{};
// Go through all values
for (size_t index{}; index < points.size(); index) {
// Check,if values are above threshold, then switch on search mode
if (not searchActive) {
if (points[index].y > thresholdMaxHigh)
searchActive = true;
}
else {
// Else, if value is lower than lower threshold, then switch of search mode formaxpeak
if (points[index].y < thresholdMaxLow)
searchActive = false;
}
// If the search is active, then find the max peak
if (searchActive)
if (points[index].y > maxPeakY) {
maxPeakX = points[index].x;
maxPeakY = points[index].y;
}
// Check for a transition from active to inactive. In that very moment, store the previosuly found values
if (not searchActive and oldSearchActive) {
peaks.push_back({ maxPeakX, maxPeakY });
maxPeakY = std::numeric_limits<double>::min();
}
// Remember for next round
oldSearchActive = searchActive;
searchActive = points[index].y > thresholdMaxHigh;
}
return peaks;
}
int main() {
// Open the sourcefile with the curve data
std::ifstream sourceFileStream{"file.txt"};
// Check, if we could open the file
if (sourceFileStream) {
// Here, we will store our curve data
Curve curve{};
// Now read all all points and store them as a curve
sourceFileStream >> curve;
// Show peaks output
for (const Point& p : curve.findPeaks()) std::cout << p << '\n';
}
else std::cerr << "\n*** Error: Could not open source file\n";
}