Rod Stephens in his book "Essential algorithms " gives some algorithm for finding of a self-avoiding walk in a lattice. It claims that

Depending on the size of the lattice and the starting point, it may be impossible to find a complete self-avoiding walk. For example, try building a walk on a lattice with two rows and three columns and starting from a point in the middle column.

But it is very easy to build a self-avoiding walk for this case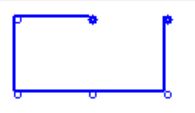 - see the image. So I'd like to ask : what is the minimal example of a lattice and a point (if exists) such that it's impossible to find a complete self-avoiding walk starting in this point?

CodePudding user response：

1xN, where N>=3 is unsolvable from any point that isn't an end.

2xN, where N>=2 is solvable from any point by making a loop.

3x3 has no self-avoiding walk starting in the middle of a side.

If you color the nodes in a checkerboard pattern with, say, black corners, then there will be 5 black nodes and 4 white nodes. Every path alternates between black and white, so if you start on white, after WBWBWBWB, you've got a black node left, but can't move because you're out of white nodes.