pandas cumsum and start again-CodePudding

I have a normal dataframe

import pandas as pd
d = {'id': [1,1,2,3,4,4,5], 'param': [11,22,33,44,55,66,77]}

df = pd.DataFrame(data=d)

I would like to create a new column and do cumsum and start again once after every second id like the following scheme:

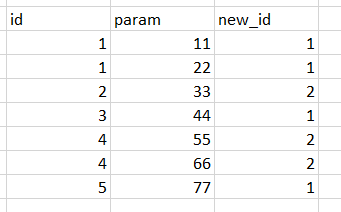
[ enter image description here

It starts with 1. Once a new value in column1 ('id) it should increase by one. Once again a new value in column 1 it should start 1 again and so on.

CodePudding user response：

I think you'd almost have to solve this one by binning the data. In this case I used qcut to create len(df) // 2 bins - 3 in this case.

If you look at the results of the qcut you can see the group labels that get generated:

pd.qcut(df.id,len(df)//2)

0    (0.999, 2.0]
1    (0.999, 2.0]
2    (0.999, 2.0]
3      (2.0, 4.0]
4      (2.0, 4.0]
5      (2.0, 4.0]
6      (4.0, 5.0]

Using this as a groupby key, we can check whether each id within each group is not equal to the id.shift, which returns a boolean value which can be used for cumsum

import pandas as pd
d = {'id': [1,1,2,3,4,4,5], 'param': [11,22,33,44,55,66,77]}

df = pd.DataFrame(data=d)

df['new_id'] = df.groupby(pd.qcut(df.id,len(df)//2)).apply(lambda x: (x.id.ne(x.id.shift())).cumsum()).values

Output

   id  param  new_id
0   1     11       1
1   1     22       1
2   2     33       2
3   3     44       1
4   4     55       2
5   4     66       2
6   5     77       1

CodePudding user response：

Alternate approach; seems to be about 3-4x faster.

2.2 ms ± 238 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
8.65 ms ± 884 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

df['new_id'] = df['id'].map(df.groupby('id').apply(lambda x: 1).cumsum().add(1).mod(2).add(1).to_dict())

   id  param  new_id
0   1     11       1
1   1     22       1
2   2     33       2
3   3     44       1
4   4     55       2
5   4     66       2
6   5     77       1

CodePudding user response：

In case id column contains adjacent integers (as in the example), you could derive the new_id columns by looking at the least significant bit of id:

df["new_id"] = 2 - np.bitwise_and(1, df.id)

If ids are more general, you can call groupby ngroup first, then reuse the above solution:

df["new_id"] = np.bitwise_and(1, df.groupby(df.id).ngroup())   1

Result:

   id  param  new_id
0   1     11       1
1   1     22       1
2   2     33       2
3   3     44       1
4   4     55       2
5   4     66       2
6   5     77       1