Recursive Euclidean GCD algorithm with function-CodePudding

I'm asking about the recursive part I have to display (and in a function with another argument verbose: bool). I need to calculate the gcd of two numbers. But how I can display the quotient and the rest and the opertions?

Like this:

By setting q the quotient of the integer division of a by b, let us calculate for example
the gcd of 90 and of 35 (gcd (90,35), so a = 90 and b = 35):
  a = b × q   r
As for 90/35 we have q = 2 and r = 20, then 90 = 35 × 2   20
According to Euclid, pgcd (90.35) = pgcd (35.20). So we start over with the new values:
  35 = 20 × 1   15
According to Euclid, pgcd (35.20) = pgcd (20.15). So we start over with the new values:
  20 = 15 × 1   5
According to Euclid, pgcd (20.15) = pgcd (15.5). So we start over with the new values:
  15 = 5 × 3   0
15 is divisible by 5 so we stop and pgcd (15.5) = pgcd (20.15) = pgcd (35.20) =
pgcd (90.35) = 5

Write the code of the euclid function (a: int, b: int, verbose: bool = False) -> int which
calculates the gcd of a and b and, if the verbose parameter is True, displays the
different steps of the algorithm of the calculation (the values of a, b, q and r).

I tried this but this is complete, I don't know anything about this. I don't even know what's the order of what.

What I've tried:

def gcd(a,b, verbose = False):
    r = a%b
    q:int

    if r == 0:
        q = a//b
        print(b)
        return b
    else:
        verbose = True
        while r != 0:
            result = b*q r
            a= result
            b = result
            r = b
        return result

num1 = int(input('chose a number'))
num2 = int(input('chose a second number'))

print(gcd(num1,num2, verbose = False))

Here's the output:

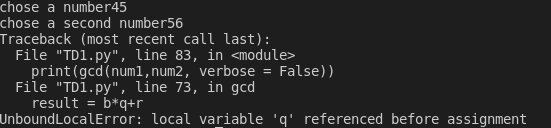
output

"before assignment" yes, but according to the problem I don't know where to put q except in if r== 0 then q = a//b.

And I don't know how to make the recursive part how I'm supposed to loop on a = b*q r and say that if r is not 0 then a is b and b is r and to do it until r is 0 and print the gcd, if verbose is True I have to describe each calculation and print a,b,r, and q.

CodePudding user response：

You can do this using a recursive approach in following fashion:

def gcd(a,b,verbose=False):
    if b>a:
        return gcd(b,a,verbose)
    r=a%b
    if r==0:
        if verbose==True:
            q=a//b
            print("a=",a,"b=",b,"q=",q,"r=",r)
        return b
    else:
        if verbose==True:
            q=a//b
            print("a=",a,"b=",b,"q=",q,"r=",r)
        return gcd(b,r,verbose)

CodePudding user response：

Your assignment doesn't say you have to use recursion and, in fact, it's simpler if you don't and use iteration (i.e. a loop) instead.

Here's what I mean:

def gcd(a: int, b: int, verbose: bool = False) -> int:
    while b != 0:
        if verbose:
            print(f'{a=}, {b=}')
        q = a // b
        r = a % b
        a = b
        b = r
    return a

#num1 = int(input('chose a number'))
#num2 = int(input('chose a second number'))
num1, num2 = 90, 35  # Hardcode for testing.

Output:

a=90, b=35
a=35, b=20
a=20, b=15
a=15, b=5
gcd(num1, num2, verbose=True)=5