Probability of a roll dice-CodePudding

I generated 1,000,000 random number draws using the random module

import random
liste = []
for i in range(0, 1000000):
liste.append(random.uniform(0,1))

Now I have to store the values obtained in a histogram at 6 bins using the bins option. And using if/else conditions on the list items, write a algorithm to simulate the result of 1,000,000 dice rolls. Then I have to calculate the frequency of occurrence of each value and compare it to the expected probability p = 1/6.

Does anyone know how to do this please I have no idea...

Thanks in advance!

edit: concerning the bins options

they talk about this :

import matplotlib.pyplot as plt
import numpy as np
# Création de la figure et des axes
fig, axs = plt.subplots(1, 1, sharey=True, tight_layout=True)
# Ajout de l'histogramme
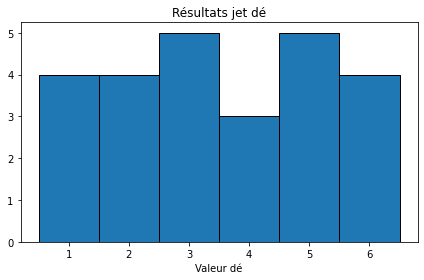
axs.hist(valeurs, bins=np.arange(0.5, 7.5, 1), ec="black")
axs.set_title("Résultats jet dé")
axs.set_xlabel("Valeur dé")

After using @Roland_Smith's program it gives me this

 #import random
 #liste = []
 #for i in range(0, 1000000):
 #    liste.append(random.uniform(0,1))
 import random
 liste = random.choices((1,2,3,4,5,6), k=1000000)
 import collections
 c = collections.Counter(liste)
 print(c)

 p = [j/1e6 for j in c.values()]
 print(p)

 import matplotlib.pyplot as plt
 import numpy as np
 # Création de la figure et des axes
 fig, axs = plt.subplots(1, 1, sharey=True, tight_layout=True)
 # Ajout de l'histogramme
 axs.hist(c, bins=np.arange(0.5, 7.5, 1), ec="black")
 axs.set_title("Résultats jet dé")
 axs.set_xlabel("Valeur dé")

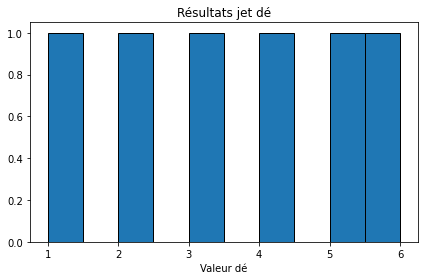
but the problem is that my histogram looks like this

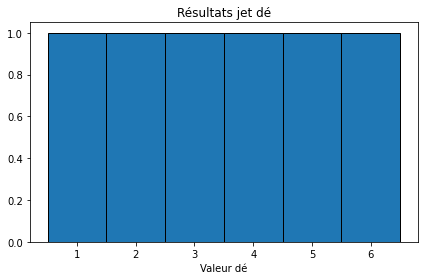
is it normal because each number has the same probability of appearing or is it not normal?

edit for tdy

import matplotlib.pyplot as plt
import numpy as np
# Création de la figure et des axes
fig, axs = plt.subplots(1, 1, sharey=True, tight_layout=True)
# Ajout de l'histogramme
axs.hist(c,ec="black")
axs.set_title("Résultats jet dé")
axs.set_xlabel("Valeur dé")

edit after help for @JohanC

#import random
#liste = []
#for i in range(0, 1000000):
#    liste.append(random.uniform(0,1))
import random
liste = random.choices((1,2,3,4,5,6), k=1000000)
import collections
c = collections.Counter(liste)
print(c)

p = [j/1e6 for j in c.values()]
print(p)

import matplotlib.pyplot as plt
import numpy as np
plt.bar(c.keys(), c.values())

# Création de la figure et des axes
#fig, axs = plt.subplots(1, 1, sharey=True, tight_layout=True)
# Ajout de l'histogramme
#axs.hist(c,ec="black")
#axs.set_title("Résultats jet dé")
#axs.set_xlabel("Valeur dé")

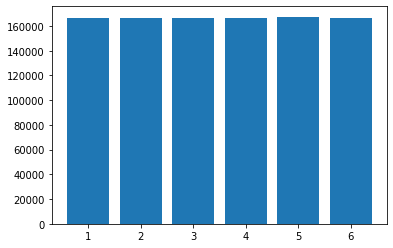
i get a value of 160000 for each dice face, i.e. 6. but 6*160000 960000 i shouldn't get the number of rolls, i.e. 1000000?

CodePudding user response：

Dice rolls produce an integer value.

So using random.uniform (which returns a float) is not the right way.

Try:

import random
liste = random.choices((1,2,3,4,5,6), k=1000000)

Then, I'd use collections.Counter to count the values:

import collections
c = collections.Counter(liste)
print(c)

This would get you something like:

Counter({6: 167399, 5: 167083, 2: 166789, 3: 166548, 1: 166236, 4: 165945})

Calculating the probability:

p = [j/1e6 for j in c.values()]

This yields:

[0.167083, 0.165945, 0.167399, 0.166789, 0.166548, 0.166236]

For plotting;

import matplotlib.pyplot as plt

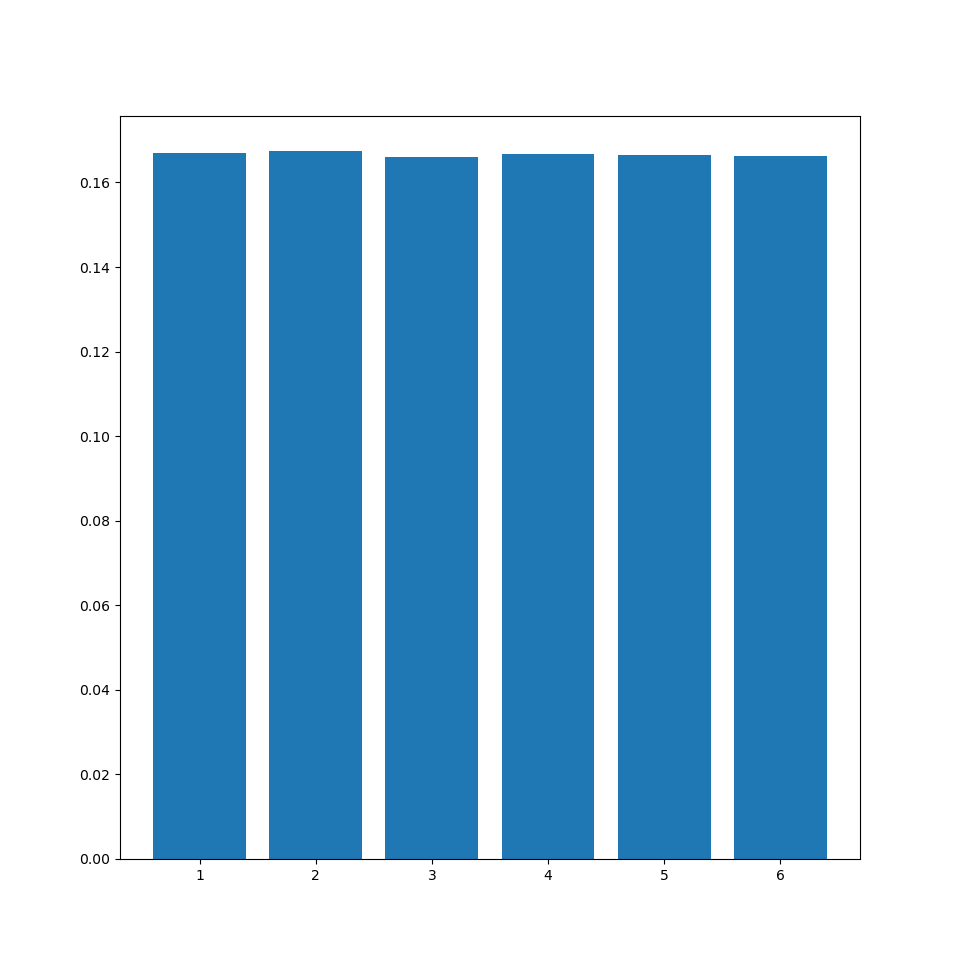
plt.bar(c.keys(),p)
plt.show()

It will look something like this:

The reason that all bars look about the same is because they are.

Let's check the difference between p and the probability of a fair dice, which is 1/6:

[round(j-1/6, 6) for j in p]

This gives:

[0.000416, -0.000722, 0.000732, 0.000122, -0.000119, -0.000431]

So the actual counted probability is pretty close to that of a fair dice.