build a parse tree from if statement-CodePudding

My goal is to be able to say if a particular JSON objects matches a particular set of rules that are stored in a .yaml file. A rule is similar to something that we can find in an if statement. For example:

if( A and B OR C):
   #do something

where A, B and C are some conditions, for example to check if one attribute of the JSON object is greater than 0 (just an example).

I would like to build the corresponding parse tree of a particular if statement. In such a tree, the nodes would be the logical operators, namely AND and OR and the leaves would be the actual conditions. Let's consider the following condition: (((A and B) OR (C AND B AND D AND E)) AND F). That would give us the following parse tree:

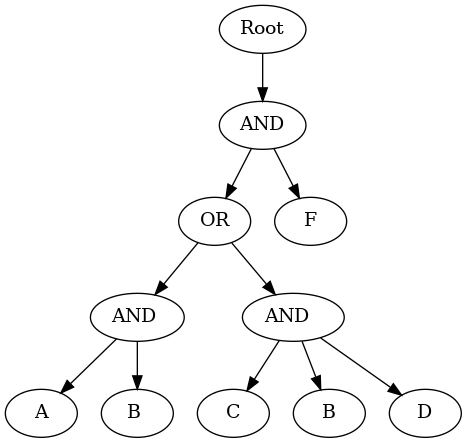
After building such a tree, one would iterate from the far left of the tree (or far right, does not matter) and start performing the tests. If we start for example in the far left of the tree, that would be the leaf A. One verifies if A is satisfied, if it is not, then the JSON object does not match the rule since its parent is an AND operator, if it does, one would move to the second test, namely the condition B. Then check the conditions C, B and D and so on until you perform all the tests.

What approach can I use to build such trees ? Are there existing parsers that I can use to achieve this ? If there is a better way to achieve this, I would like to hear it. Thank you!

CodePudding user response：

You will indeed need to parse the text in some way.

I would suggest relying on a regular expression to tokenise the input, so that you get the following tokens:

(
)
AND
OR
Anything else will be considered an atomic condition.

Then iterate those tokens and use a stack or recursion to build the tree.

From your other questions I see you use Python, so in Python you could create a class for each operator (OR, AND) and let it inherit from list. Such a list will either have as members strings (leaves of the tree) or more OR or AND list instances. So the whole tree is actually a nested list structure.

Here is how you would implement those list-based classes:

# A generic class from which all operators derive
class Node(list):
    @property
    def label(self):
        return self.__class__.__name__

    def __repr__(self):
        return self.label   super().__repr__()

# Subclass for each operator: no additional logic is needed 
class AND(Node): pass
class OR(Node): pass

Here is the parser:

import re

def parse(s):
    # Rely completely on the operators that have been defined as subclasses of Node
    Operators = { cls.__name__ : cls for cls in Node.__subclasses__() }
    # Create a regular expression based on those operator names (AND, OR)
    regex = r"\s*([()]|"   "|".join(fr"\b{operator}\b" for operator in Operators.keys())   ")\s*"
    # Tokenise the input
    tokens = iter((token for token in re.split(regex, s, flags=re.IGNORECASE) if token))
    
    def dfs(end=")"):
        operator = ""
        operands = []
        while True:
            token = next(tokens, "")
            if not token or token == ")":
                raise ValueError(f"Operand expected, but got '{token}'")
            operands.append(dfs() if token == "(" else token)
            token = next(tokens, "")
            if token == end:
                return Operators[operator](operands) if operator else operands[0]
            utoken = token.upper()
            if utoken in Operators:
                if operator and utoken != operator:
                    raise ValueError("Use parentheses to indicate operator precedence")
                operator = utoken
            else:
                raise ValueError(f"{', '.join(Node.keys())} expected, but got '{token}'")
    return dfs("")

Use it as follows:

# Example run
s = "(((A and B) OR (C AND B AND D AND E)) AND F)"
tree = parse(s)
print(tree)
# Demo on how to address specific nodes in the tree
print(tree.label, tree[0].label, tree[0][0].label, tree[0][0][0])