what is the easiest way to create random points on a circle of specific radius with noise in R? is there a library that does this kind of things?

CodePudding user response：

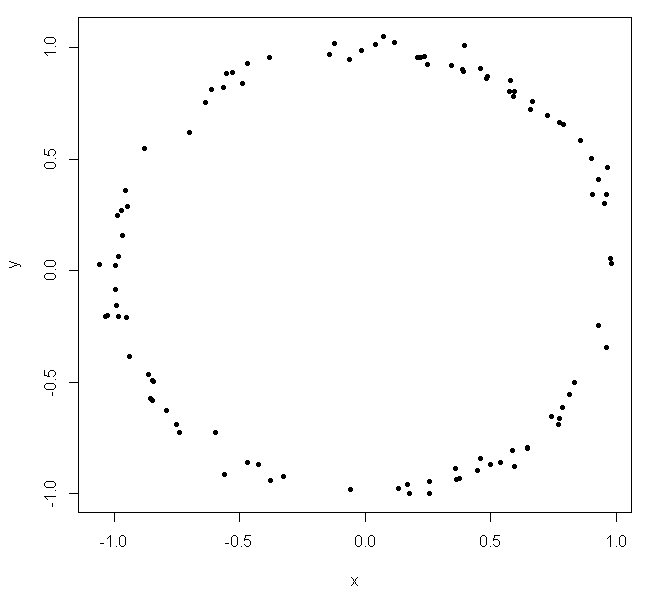
theta = runif(100, 0,2*pi)
x = cos(theta)   rnorm(100, 0, 0.03)
y = sin(theta)   rnorm(100, 0, 0.03)
plot(x,y, pch=20)

CodePudding user response：

It would be more natural to sample:

• the polar angle theta from a uniform distribution supported on [0, 2*pi),
• the polar radius r from a lognormal distribution supported on (0, Inf), so that log(r) is normally distributed with mean meanlog and standard deviation sdlog.

So you could try something like this:

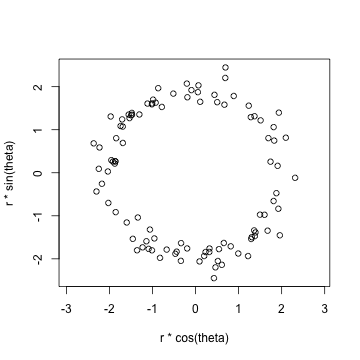
set.seed(1L)
n <- 100L
theta <- runif(n, 0, 2 * pi)
r <- rlnorm(n, meanlog = log(2), sdlog = 0.1)
plot(r * cos(theta), r * sin(theta), asp = 1)

And you could generalize to multiple circles like so:

circles <- function(n, mu, sigma) {
    lr <- Map(rlnorm, n = n, meanlog = mu, sdlog = sigma)
    N <- length(lr)
    n <- lengths(lr, FALSE)
    data.frame(group = rep.int(gl(N, 1L), n),
               r = unlist(lr, FALSE, FALSE),
               theta = runif(sum(n), 0, 2 * pi))
}

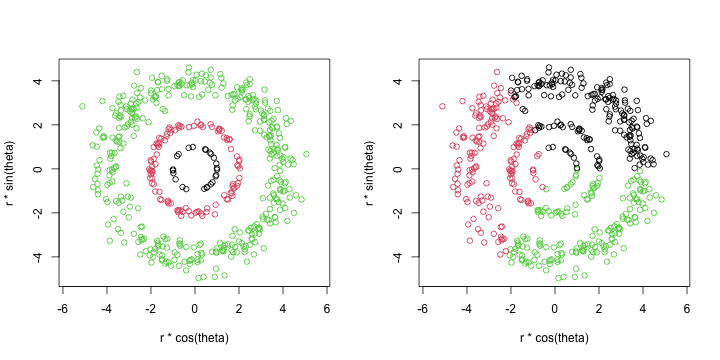
set.seed(1L)
d <- circles(n = c(25L, 100L, 400L), mu = log(c(1, 2, 4)), sigma = c(0, 0.05, 0.1))
str(d)
## 'data.frame':    525 obs. of  3 variables:
##  $ group: Factor w/ 3 levels "1","2","3": 1 1 1 1 1 1 1 1 1 1 ...
##  $ r    : num  1 1 1 1 1 1 1 1 1 1 ...
##  $ theta: num  3.335 4.303 2.408 6 0.744 ...

par(mfrow = c(1L, 2L))
with(d, {
    plot(r * cos(theta), r * sin(theta), asp = 1, col = group)
    plot(r * cos(theta), r * sin(theta), asp = 1, col = cut(theta, 0:3 * 2 * pi / 3))
})

The function circles is vectorized in n, mu, and sigma, where n is the number of points in a circle and mu and sigma are the mean and standard deviation of the log radius.