How to get eigenvectors from PCA-CodePudding

I'm using FactoMineR's PCA function to compute the PCA of my dataset.

I know I can get the eigenvalues with get_eigenvalue(res.pca) but how do I get the eigenvectors?

CodePudding user response：

In Principal Components Analysis, you're decomposing the n-by-k variable matrix into three parts - U, D and V. U are the left singular vectors that represent the rows of the decomposed matrix. However, the U matrix is not itself the principal components. All of the columns of U are mutually orthogonal (as you would expect), but they also all have the same variance. The principal components are U scaled by the square root of the eigenvalues. Here's an example:

library(FactoMineR)
data(decathlon)
dat <- decathlon[,1:10]
p <- PCA(dat)
#> Warning: ggrepel: 1 unlabeled data points (too many overlaps). Consider
#> increasing max.overlaps

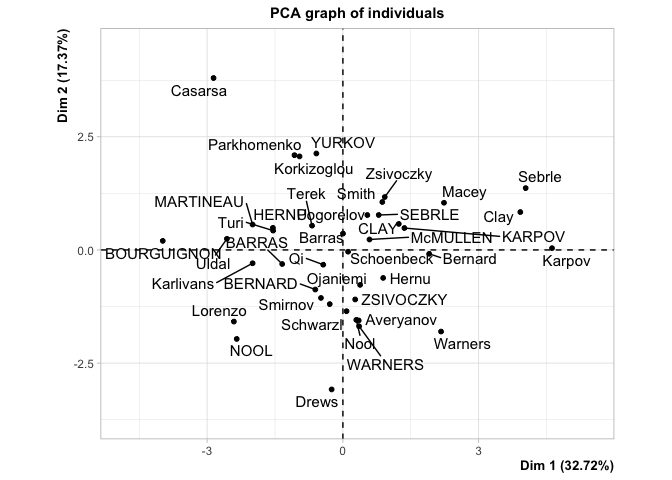
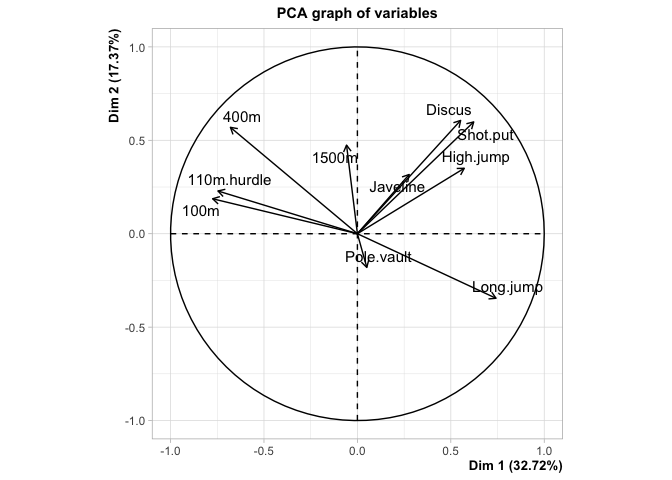
comp1 <- predict(p, newdata=dat)$coord[,1:3]

U <- p$svd$U
e <- p$eig[,"eigenvalue"]
  
comp2 <- U[,1:3] %*% diag(sqrt(e[1:3]))

head(comp1[,1:3])
#>              Dim.1      Dim.2      Dim.3
#> SEBRLE   0.7916277  0.7716112  0.8268412
#> CLAY     1.2349906  0.5745781  2.1412470
#> KARPOV   1.3582149  0.4840209  1.9562580
#> BERNARD -0.6095151 -0.8746285  0.8899407
#> YURKOV  -0.5859683  2.1309542 -1.2251568
#> WARNERS  0.3568895 -1.6849567  0.7665531
head(comp2[,1:3])
#>            [,1]       [,2]       [,3]
#> [1,]  0.7916277  0.7716112  0.8268412
#> [2,]  1.2349906  0.5745781  2.1412470
#> [3,]  1.3582149  0.4840209  1.9562580
#> [4,] -0.6095151 -0.8746285  0.8899407
#> [5,] -0.5859683  2.1309542 -1.2251568
#> [6,]  0.3568895 -1.6849567  0.7665531

^{Created on 2022-02-16 by the reprex package (v2.0.1)}