Understand Adam optimizer intuitively-CodePudding

According the pseudo code of Adam:

I wrote some code:

from matplotlib import pyplot as plt
import numpy as np
# np.random.seed(42)
num = 100

x = np.arange(num).tolist()
# The following 3 sets of g_list stand for 3 types of gradient changes:
# g_list = np.random.normal(0,1,num)  # gradient direction changes frequently in positive and negtive 
# g_list = x  # gradient direction always positive and gradient value becomes larger gradually
g_list = [10 for _ in range(num)]  # gradient direction always positive and gradient value always the same

m = 0
v = 0
beta_m = 0.9
beta_v = 0.999
m_list = []
v_list = []

for i in range(1,num 1):
    g = g_list[i-1]
    m = beta_m*m   (1 - beta_m)*g
    m = m/(1-beta_m**i)
    v = beta_v*v   (1 - beta_v)*(g**2)
    v = v/(1-beta_v**i)
    m_list.append(m)
    v_list.append(np.sqrt(v))

mv = np.array(m_list)/(np.array(v_list)  0.001)
print("==>> mv: ", mv)
plt.plot(x, g_list, x, mv)

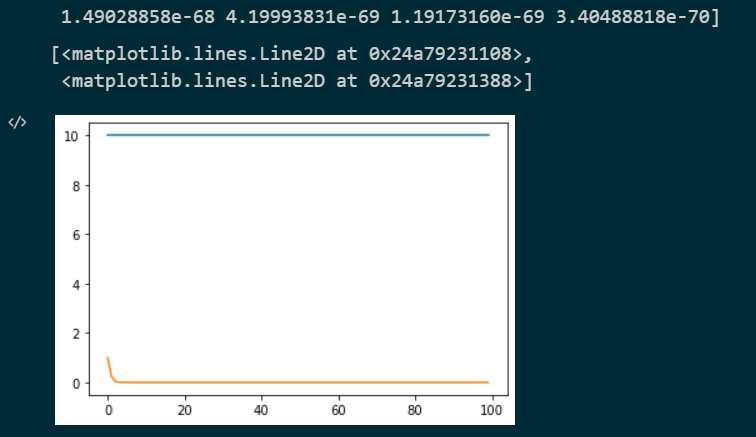
Run the code, i got following plot:

For me, I think it's counter-intuitive, because I think that when the gradient direction is always positive, and the gradient value is constant, the coefficient of the learning rate(i.e. mv) should be close to 1, but the 100th mv I got is 3.40488818e-70 which is nearly close to zero.

If I change the some of the code:

    # m = m/(1-beta_m**i)
    if i == 1:
      m = m/(1-beta_m**i)
    # v = v/(1-beta_v**i)
    if i == 1:
       v = v/(1-beta_v**i)

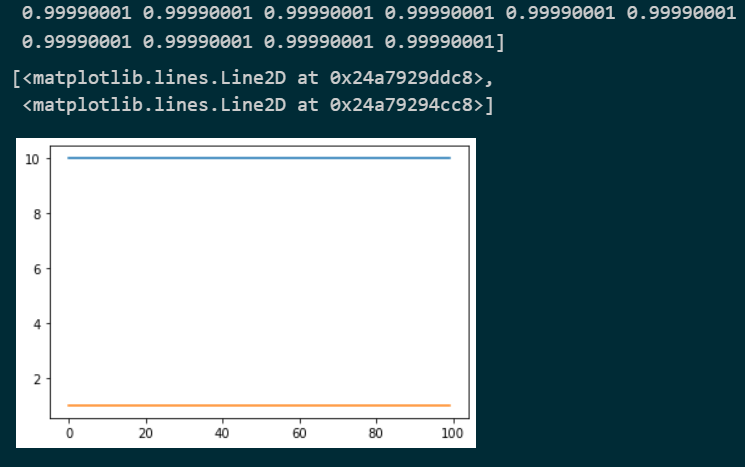
the result I get is this:

This is more in line with my intuition.

Can someone tell me if my code above is correct, and if correct, does it fit your intuition to get something like above ?

CodePudding user response：

Your code implementation is almost there, but one difference you should note between your implementation and the algorithm is that you are erroneously accumulating the bias correction term m/(1-beta_m**i) with the variable m. You should assign a separate variable m_hat for bias correction.

The same applies to v: assign the bias corrected value to another variable like v_hat.

Doing this will avoid including the bias correction in the accumulation of m and v.

Your code can stay the same, but change the calculation of the bias corrected values along with the list appends. If you do this, you will get the result you're after.

for i in range(1,num 1):
    g = g_list[i-1]

    # calculate m and v
    m = beta_m*m   (1 - beta_m)*g
    v = beta_v*v   (1 - beta_v)*(g**2)

    # assign bias corrected values to m_hat and v_hat respectively
    m_hat = m/(1-beta_m**i)
    v_hat = v/(1-beta_v**i)

    # append to lists
    m_list.append(m_hat)
    v_list.append(np.sqrt(v_hat))