Implement "Block tumbling logic" in a numpy array-CodePudding

I am using a numpy array to model iron ore falling through a bunker.

As ore is extracted from the bottom of the bunker and is added to the top, it leaves an empty space represented as a nan. I am looking to model the ore falling vertically into the spaces created.

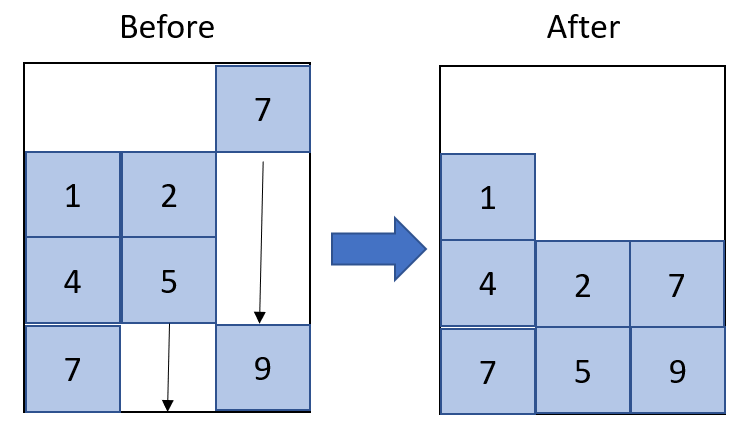
A simplified version of the array is below. The bunker is actually modelled in 3D, with a fourth dimension containing information about various features of the ore, but the 2D array illustrates the concept.

I want each column to "collapse" into the nan values as shown and add new nans at the top to represent empty space left behind. I realise that I could do this by splitting the array into columns, dropping the nan values and adding more nans to the top one column at a time, but given the size of the array to be traversed, I'm wondering if there is a way to vectorise this "vertical collapse" operation across the whole array?

import numpy as np
from numpy import nan

# The input array has some columns "hanging" above nans
arr_input = np.array(
    [[nan, nan,  7.],
     [ 1.,  2., nan],
     [ 4.,  5., nan],
     [ 7., nan,  9.]]
)

# Drop each column into the nans and add nans at the top to keep the shape the same
arr_expected = np.array(
    [[nan, nan,  nan],
     [ 1., nan,  nan],
     [ 4.,  2.,  7.],
     [ 7.,  5.,  9.]]
)

CodePudding user response：

The idea is to sort the array column by column, but instead of on value, we sort on boolean np.isnan(arr) so the nan "floats" to top, similar to the idea of bubble sort. You probably want to investigate more on the kind argument of numpy.argsort to make sure the original order are always preserved since we have duplicates in the boolean array. I think the default quicksort is not stable.

import numpy as np
from numpy import nan

arr = np.array(
    [[nan, nan,  7.],
     [ 1.,  2., nan],
     [ 4.,  5., nan],
     [ 7., nan,  9.]]
)


# the sorted are the ordered row index with nan on top
# the column index are just created to fit numpy's indexing rules
arr[np.argsort(~np.isnan(arr), axis=0, kind='mergesort'), 
    np.repeat(np.arange(arr.shape[1]).reshape(1,-1), arr.shape[0], axis = 0)]

output:

array([[nan, nan, nan],
       [ 1., nan, nan],
       [ 4.,  2.,  7.],
       [ 7.,  5.,  9.]])

On my first (unsuccessful) try of the problem, I found a solution to simulate it "step by step" (fall one block at a time):

arr_empty = np.isnan(arr)
idx_move = (~arr_empty[:-1, :]) & arr_empty[1:, :]
idx_move = np.maximum.accumulate(idx_move[::-1])[::-1]
arr[1:][idx_move] = arr[:-1][idx_move]
arr[0, idx_move.any(axis = 0)] = np.nan

output:

array([[nan, nan, nan],
       [ 1., nan,  7.],
       [ 4.,  2., nan],
       [ 7.,  5.,  9.]])

CodePudding user response：

I came up with the following, although it is not vectorised.

import numpy as np
from numpy import nan

arr_input = np.array(
    [[nan, nan,  7.],
     [ 1.,  2., nan],
     [ 4.,  5., nan],
     [ 7., nan,  9.]]
)
arr_expected = np.array(
    [[nan, nan,  nan],
     [ 1., nan,  nan],
     [ 4.,  2.,  7.],
     [ 7.,  5.,  9.]]
)

# Split out the array into columns using np.split (for loop line)
# Remove the non-nans from the column, then pad the top to fill
# Stack the result along axis 1 to get the original shape back
arr_output = np.stack([
    np.pad(
        col[~np.isnan(col)], 
        (np.isnan(col).sum(), 0), # Pad at top
        'constant', 
        constant_values=np.nan
    )
    for col in np.split(arr_input, arr_input.shape[1], axis=1)
], axis=1)

np.testing.assert_almost_equal(arr_output, arr_expected)