If i apply a window to my time domain transient signal i convoulte the temporal signal spectrum with the spectrum of the window function. If i use no window i convolute the signal with the spectrum of a rectangular window.
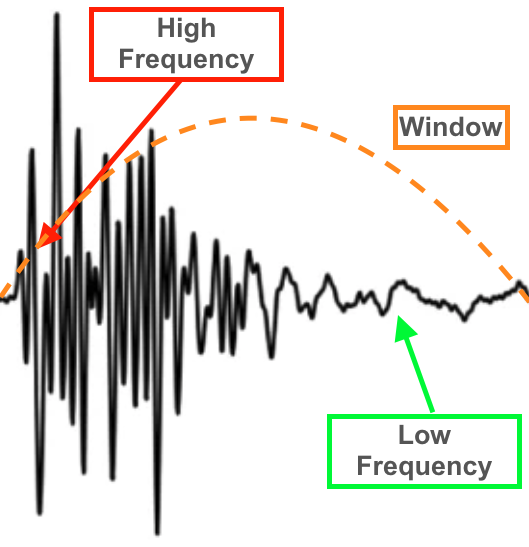
What i have is a transient signal with differing temporal spectral bandpower, meaning high frequencies are at the beginning of the signal and low frequencies are at the middle and end. But this can also change. Now if i multiply my time domain signal with a hann window the amplutide of the beginning and the end will be substantially damped due to the window but if i use no window (rectangular) the spektrum will be broadend and my energies will be wrong too.
What i want to have is the most accurate band powers, which window is the best for this application?
CodePudding user response:
If you are working with a real data flow, the FFT should have some sort of overlap (to help address your concerns about missing something). For the audio analysis I'm currently working on, I like to use a minimum overlap of 15%
Based on the original description, if you are given one snapshot of data and asked to analyze it, there are techniques you use to get around the real problem you described. You can add your own padding or (my favorite) replicate the data within a larger FFT (if your primary interest is magnitude and not phase, you can implement a mirroring approach to address edge discontinuities).
CodePudding user response:
As you say, when you multiply the signal by the window, you convolve the signal's FFT with the window's FFT.
Both of these FFTs are complex, however, and what the above statement neglects is that, because of the phase relationship between the window and the signal, this convolution will attenuate the frequencies that occur near the window ends.
The windowing procedure doesn't seem to be appropriate for what you're doing. You basically have two choices:
You can use multiple overlapping windows, as J.R. says in his answer. Overlap by 50% and average the power spectra.
Instead of windowing, you can pad your signal out with zeros to 4x or 8x its original length, and then do an FFT of the whole thing. This will give you more resolution in your FFT and, because a time-limited signal has a band-limited Fourier transform, the FFT will be pretty smooth and you can use cubic interpolation to give you a good approximation of the actual continuous Fourier transform of your signal.
