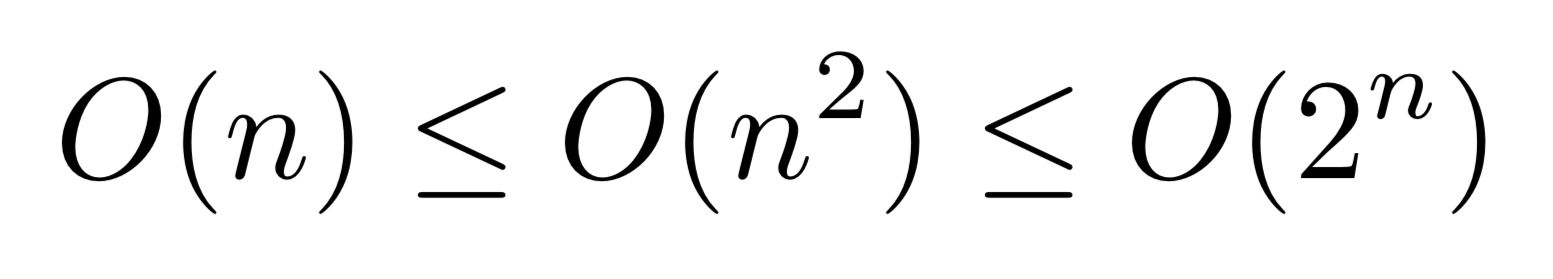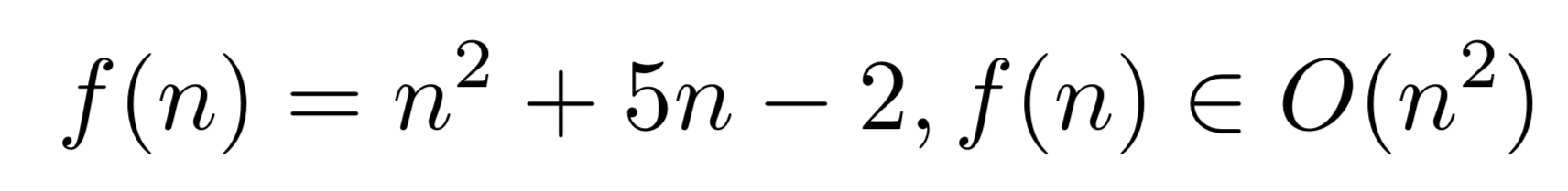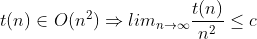I‘m trying to wrap my head around the meaning of the Landau-Notation in the context of analysing an algorithm‘s complexity.

What exactly does the O formally mean in Big-O-Notation?

So the way I understand it is that O(g(x)) gives a set of functions which grow as rapidly or slower as g(x), meaning, for example in the case of O(n^2):

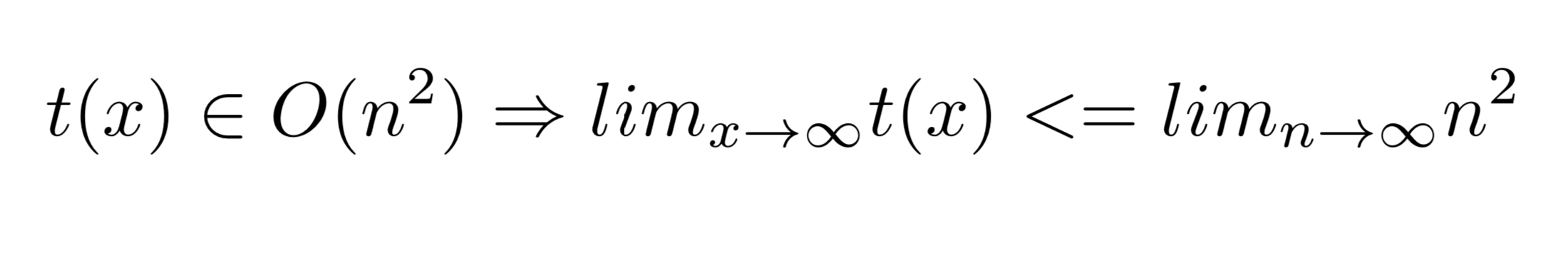where t(x) could be, for instance, x 3 or x^2 5. Is my understanding correct?

Furthermore, are the following notations correct?

I saw the following written down by a tutor. What does this mean? How can you use less or equal, if the O-Notation returns a set?

Could I also write something like this?

CodePudding user response：

So the way I understand it is that O(g(x)) gives a set of functions which grow as rapidly or slower as g(x).

This explanation of Big-Oh notation is correct.

f(n) = n^2 5n - 2, f(n) is an element of O(n^2)

Yes, we can say that. O(n^2) in plain English, represents "set of all functions that grow as rapidly as or slower than n^2". So, f(n) satisfies that requirement.

O(n) is a subset of O(n^2), O(n^2) is a subset of O(2^n)

This notation is correct and it comes from the definition. Any function that is in O(n), is also in O(n^2) since growth rate of it is slower than n^2. 2^n is an exponential time complexity, whereas n^2 is polynomial. You can take limit of n^2 / 2^n as n goes to infinity and prove that O(n^2) is a subset of O(2^n) since 2^n grows bigger.

O(n) <= O(n^2) <= O(2^n)

This notation is tricky. As explained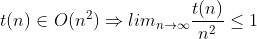

This is incorrect: the ratio only has to be less than or equal to some fixed constant c > 0.

Here is the correct version:

where c is some fixed positive real number, that does not depend on n.

For example, f(x) = 3 (n^2) is in O(n^2): one constant c that works for this f is c = 4. Note that the requirement isn't 'for all c > 0', but rather 'for at least one constant c > 0'

The rest of your remarks are accurate. The <= signs in that expression are an unusual usage, but it's true if <= means set inclusion. I wouldn't worry about that expression's meaning.

There's other, more subtle reasons to talk about 'boundedness' rather than growth rates. For instance, consider the cosine function. |cos(x)| is in O(1), but its derivative fluctuates from negative one to positive one even as x increases to infinity.

If you take 'growth rate' to mean something like the derivative, example like these become tricky to talk about, but saying |cos(x)| is bounded by 2 is clear.

For an even better example, consider the