Optimize trivial summation in calculation of geometric distribution-CodePudding

I have the following function:

def geo_dist_names(p, k):
    sum = 0
    for i in range(1, 4):
        sum  = p**i   
    return (p**(1 k))/sum

p is a float between 0 and 1 and k is an int between 0 and 3. The function basically just find the value in a geometric distribution associated with the given p and k and then normalizes this by dividing with the sum of the 4 potential values for k.

It works, but I am calling this function many times so I wondered if there were a more optimized and/or cleaner way of performing this operation?

CodePudding user response：

Don't know if it's more optimized. But as a one-liner you can wright it like this:

def geo_dist_names(p, k):
    return (p**(1 k))/(p p**2 p**3)

CodePudding user response：

The vectorial version of your code would be:

import numpy as np

def geo_dist_names(p, k):
    return (p**(1 k))/(p**np.arange(1,4)).sum()

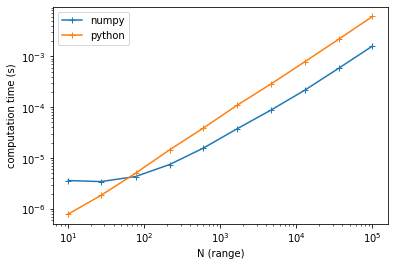
Yet, I'm not sure that it will be faster than pure python as the range is quite small here, so the overhead of numpy is probably not negligible.

Edit. Indeed, assuming:

def geo_dist_names_python(p, k, N=4):
    sum = 0
    for i in range(1, N):
        sum  = p**i   
    return (p**(1 k))/sum

def geo_dist_names_numpy(p, k, N=4):
    return (p**(1 k))/(p**np.arange(1,N)).sum()

numpy is better only when the range increases: