I came across the following problem.

You are given the root of a binary tree with n nodes. 
Each node is uniquely assigned a value from 1 to n. 
You are also given an integer startValue representing 
the value of the start node s, 
and a different integer destValue representing 
the value of the destination node t.

Find the shortest path starting from node s and ending at node t. 
Generate step-by-step directions of such path as a string consisting of only the 
uppercase letters 'L', 'R', and 'U'. Each letter indicates a specific direction:

'L' means to go from a node to its left child node.
'R' means to go from a node to its right child node.
'U' means to go from a node to its parent node.
Return the step-by-step directions of the shortest path from node s to node t

Example 1:

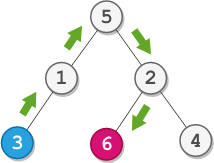
Input: root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6
Output: "UURL"
Explanation: The shortest path is: 3 → 1 → 5 → 2 → 6.

Example 2:

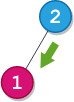
Input: root = [2,1], startValue = 2, destValue = 1
Output: "L"
Explanation: The shortest path is: 2 → 1.

I created the solution by finding the least common ancestor and then doing a depth-first-search to find the elements, Like this:-

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def getDirections(self, root, startValue, destValue):
        """
        :type root: Optional[TreeNode]
        :type startValue: int
        :type destValue: int
        :rtype: str
        """

        def lca(root):
            if root == None or root.val == startValue or root.val == destValue:
                return root
        
            left = lca(root.left)
            right = lca(root.right)
        
            if left and right:
                return root
        
            return left or right
    
        def dfs(root, value, path):
            if root == None:
                return ""
        
            if root.val == value:
                return path
        
            return dfs(root.left, value, path   "L")   dfs(root.right, value, path   "R")
        
        
        root = lca(root)
        return "U"*len(dfs(root, startValue, ""))   dfs(root, destValue, "")
    

The solution runs good, however for a very large input it throws "Memory Limit Exceeded" error, can anyone tell me how I can optimise the solution, or what might I be doing that could be getting me into it ?

CodePudding user response：

The reason you're getting a memory limit exceeded is the arguments to the dfs function. Your 'path' variable is a string that can be as large as the height of the tree (which can be the size of the whole tree if it's unbalanced).

Normally that wouldn't be a problem, but path "L" creates a new string for every recursive call of the function. Besides being very slow, this means that your memory usage is O(n^2), where n is the number of nodes in the tree.

For example, if your final path is "L" * 1000, your call stack for dfs will look like this:

Depth 0: dfs(root, path = "")
Depth 1: dfs(root.left, path = "L")
Depth 2: dfs(root.left.left, path = "LL")
...
Depth 999:  path = "L"*999
Depth 1000:  path = "L"*1000

Despite all those variables being called path, they are all completely different strings, for a total memory usage of ~(1000*1000)/2 = 500,000 characters at one time. With one million nodes, this is half a trillion characters.

Now, this doesn't happen just because strings are immutable; in fact, even if you were using lists (which are mutable), you'd still have this problem, as path ["L"] would still be forced to create a copy of path.

To solve this, you need to have exactly one variable for the path stored outside of the dfs function, and only append to it from the recursive dfs function. This will ensure you only ever use O(n) space.

def dfs(root, value, path):
    if root is None:
        return False

    if root.val == value:
        return True

    if dfs(root.left, value, path):
        path.append("L")
        return True
    elif dfs(root.right, value, path):
        path.append("R")
        return True
    return False

root = lca(root)
start_to_root = []
dfs(root, startValue, start_to_root)

dest_to_root = []
dfs(root, destValue, dest_to_root)

return "U" * len(start_to_root)   ''.join(reversed(dest_to_root))