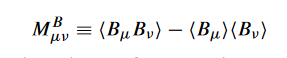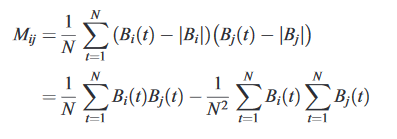I have two 3d column vectors B_mu and B_nu that vary as a function of time:

import numpy as np
N = 5 # 5 time-steps

B_mu = np.array(
      [[5, 5, 8],
       [4, 8, 7],
       [2, 3, 1],
       [5, 7, 8],
       [6, 2, 7]]
)
B_nu = np.array(
      [[3, 2, 9],
       [9, 8, 8],
       [4, 9, 9],
       [4, 9, 6],
       [1, 9, 1]]
)

For every index i in the first vector, and every index j in the second vector, I want to compute the difference between the time-average of the product < B_mu[i] B_nu[j] > and the product of the time-averages <B_mu[i]> <B_nu[j]>.

In other words, I want to construct the matrix M such that:

M[i,j] = 1/N sum(B_mu[i] * B_nu[j]) - 1/N**2 * sum(B_mu[i]) * sum(B_nu[j])

where the sums are taken over the time parameter.

Here is the equation:

And an explicit, expanded version:

How can I express this equation in python?

CodePudding user response：

Manipulation of matrices is relatively easy with module numpy. Here we're looking for:

• averaging (or summing) over one dimension (time);
• taking the outer product of two column vectors.

We're going to use:

• method array.sum with the optional axis parameter to sum over the time dimension;
• function outer.

These two functions combine straightforwardly to compute the product of averages. The average of the products, on the other hand, is straightforward to compute with python builtins sum and map; I don't know how to do it in pure numpy.

import numpy as np

def diff_avgprod_prodavg(B_mu, B_nu):
    N = B_mu.shape[0]
    avg_of_prod = 1/N * sum(map(np.outer, B_mu, B_nu)) # not pure numpy
    prod_of_avg = 1/(N*N) * np.outer(B_mu.sum(axis=0), B_nu.sum(axis=0))
    return avg_of_prod - prod_of_avg

Testing:

B_mu = np.array(
      [[5, 5, 8],
       [4, 8, 7],
       [2, 3, 1],
       [5, 7, 8],
       [6, 2, 7]]
)
B_nu = np.array(
      [[3, 2, 9],
       [9, 8, 8],
       [4, 9, 9],
       [4, 9, 6],
       [1, 9, 1]]
)

print( diff_avgprod_prodavg(B_mu, B_nu) )
# [[-1.48 -0.76 -2.84]
#  [ 4.8  -0.6   3.  ]
#  [-0.04 -2.68 -2.52]]

print( diff_avgprod_prodavg(B_mu, B_mu) )
# [[1.84 0.   3.12]
#  [0.   5.2  2.8 ]
#  [3.12 2.8  6.96]]

print( diff_avgprod_prodavg(B_nu, B_nu) )
# [[ 6.96  0.72  4.28]
#  [ 0.72  7.44 -3.64]
#  [ 4.28 -3.64  9.04]]