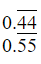Is there a way to take into account the periodic decimals in my function, for example:

So instead of just having a function y * 0.44 or y * 0.55 the program would use as many decimals as possible: y * 0.44444444 or y * 0.55555555 in its calculations.

One way I think would be by looping through the decimals and adding .0 as many times as possible. However, is there a leaner way?

CodePudding user response：

You could try defining the repeating values with fractional notation

point4=4/9   #0.4444444444...
point5=5/9    #0.5555555555...

y * point4
y * point5

To generalize to any repeating number, divide your number "n" with another number where every digit of "n" is replaced by 9

ex. 26/99 -> 0.26262626...

ex. 10203/99999 -> 0.102031020310203...

CodePudding user response：

This is a misunderstanding of how floats work. They have a limited size (usually 32 or 64 bits) and precision (they store a number using an exponent and a binary expansion).

So if you want to represent a number with infinite precision it is impossible with floats. You probably need to use a symbolic representation instead.

Even if you want to use the most decimal places possible, it is still a problem, because floats work in binary and not decimal, so there is no equal number of precise decimal places for every float. (for more information about floats see Wikipedia)

The best alternative I can think of, if you only need rational numbers, could be using the fractions module.

In [1]: from fractions import Fraction

In [2]: Fraction(3, 4) * Fraction(5, 3)
Out[2]: Fraction(5, 4)

If you need more advanced stuff, you could try sympy.

CodePudding user response：

One comment solved it:

0.44 --> 44/99 --> 0.44444444

0.58 --> 58/99 --> 0.58585858

0.4 --> 4/9 --> 0.44444

0.567 --> 567/999 --> 0.567567567