How can I create an age-stratified linear regression?-CodePudding

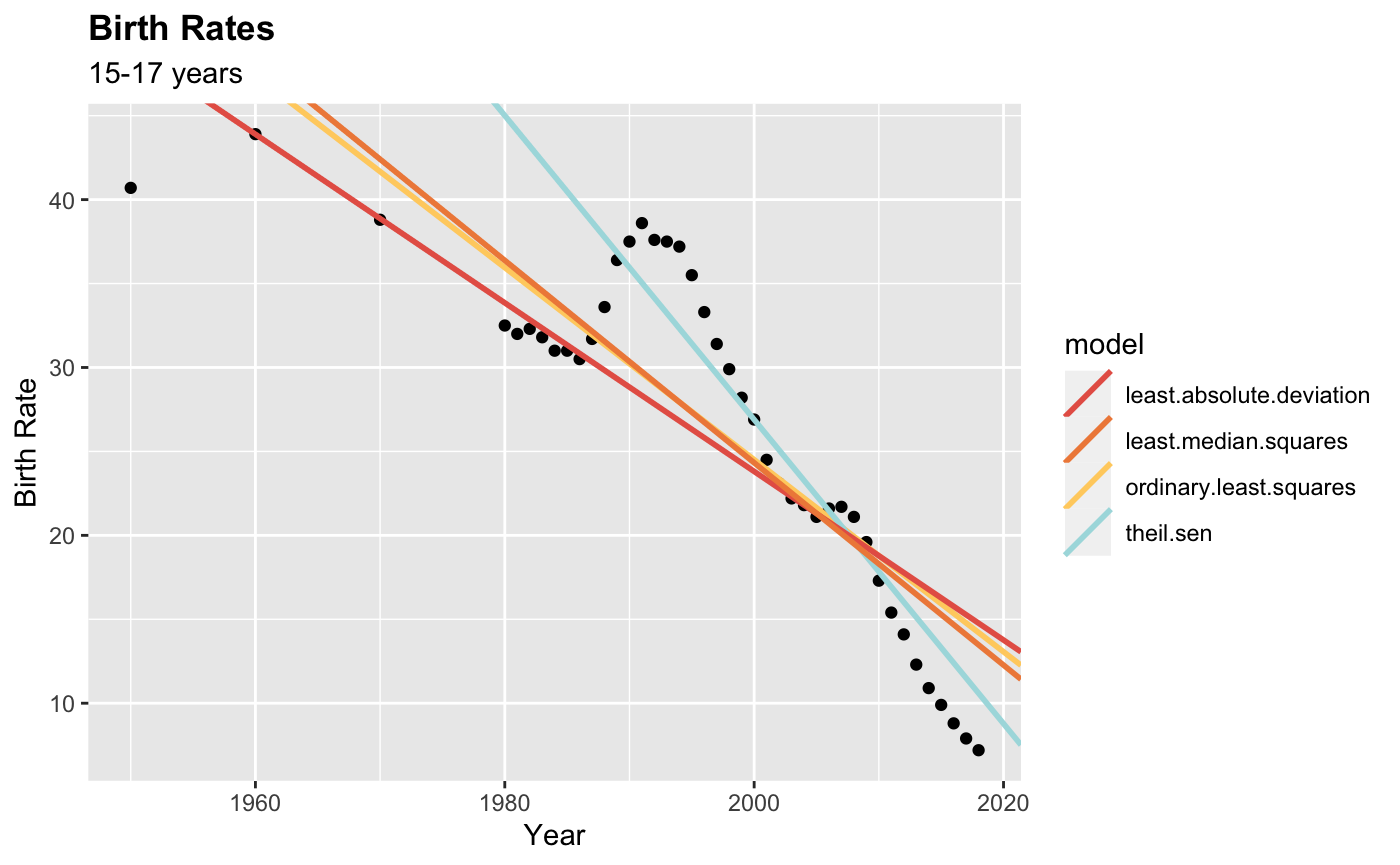
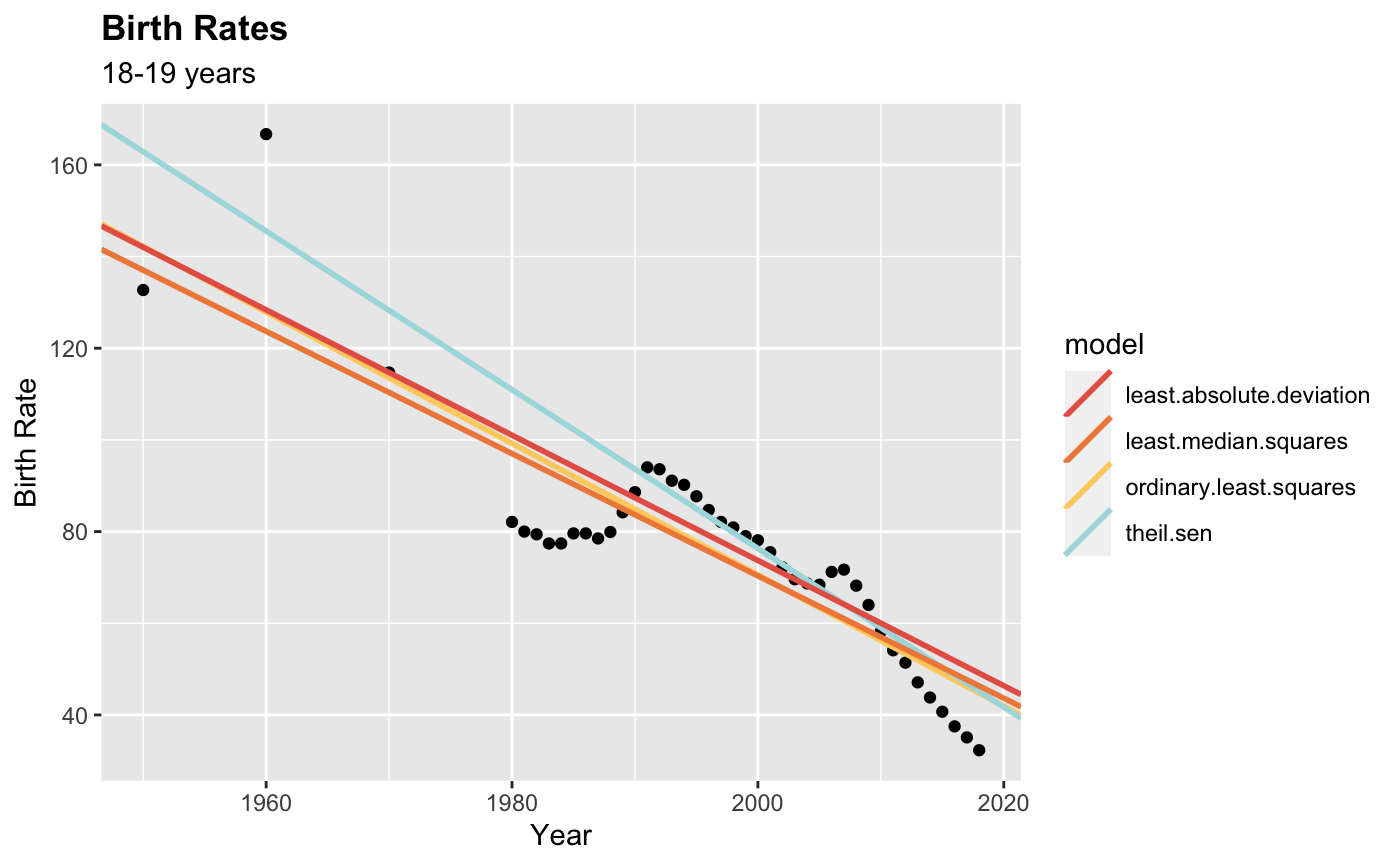
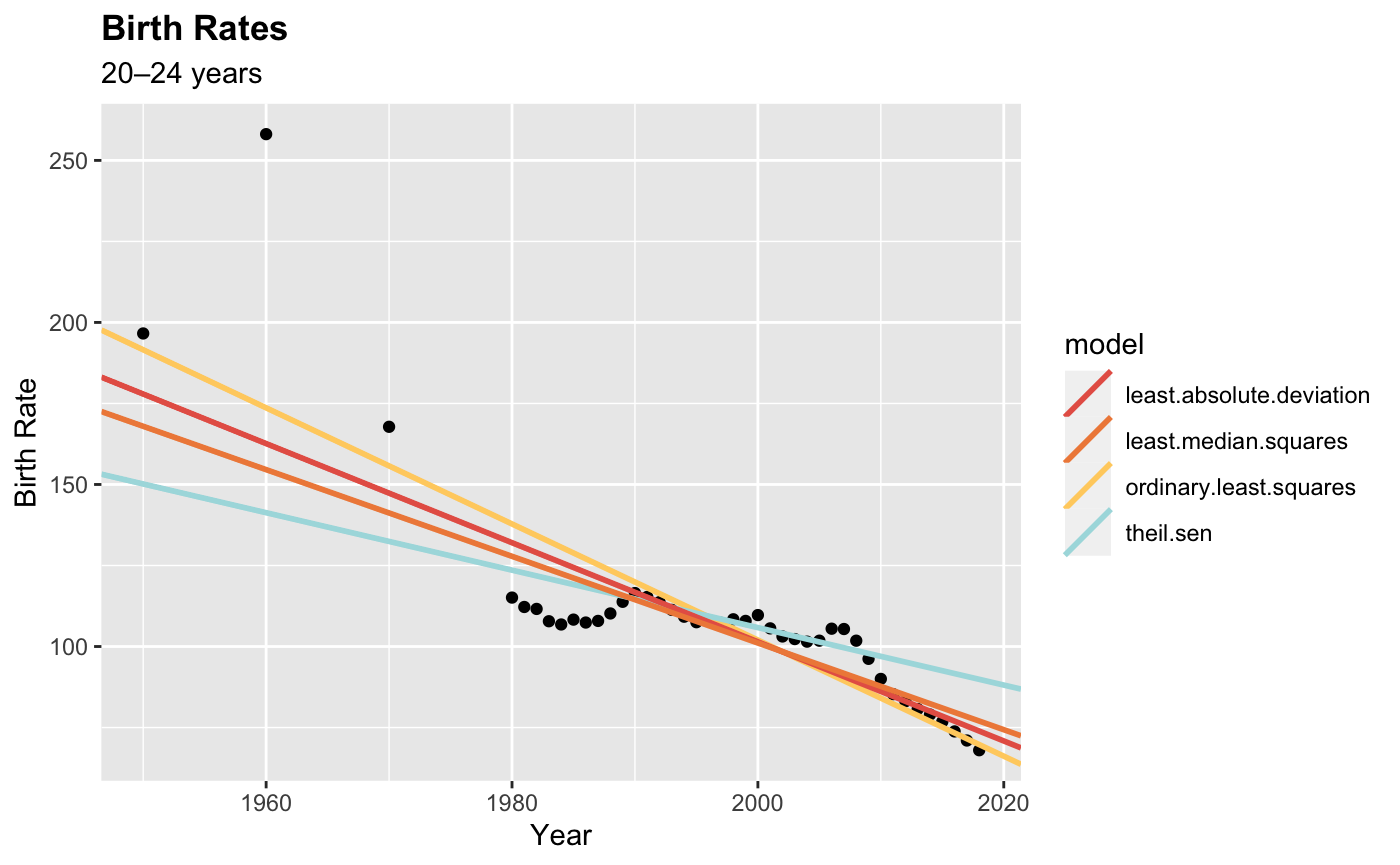
I want to do some predictive modeling with a linear regression, where the Year is the independent variable and each age bracket (15-17 years, 18-19 years, 20–24 years, etc) is the dependent variable. I would like to predict the birth rates for each age group based on historical data (predict birth rates for each age group into 10 years into the future). The data within each age bracket variable represents birth rates. The Crude Birth Rate variable can be ignored for the purposes of this analysis, as I want to perform the analysis within each age bracket (rather than aggregated).

My data are below:

> dput(age)
structure(list(Year = c(1950, 1960, 1970, 1980, 1981, 1982, 1983, 
1984, 1985, 1986, 1987, 1988, 1989, 1990, 1991, 1992, 1993, 1994, 
1995, 1996, 1997, 1998, 1999, 2000, 2001, 2002, 2003, 2004, 2005, 
2006, 2007, 2008, 2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 
2017, 2018, NA), `Crude Birth Rate` = c(24.1, 23.7, 18.4, 15.9, 
15.8, 15.9, 15.6, 15.6, 15.8, 15.6, 15.7, 16, 16.4, 16.7, 16.2, 
15.8, 15.4, 15, 14.6, 14.4, 14.2, 14.3, 14.2, 14.4, 14.1, 14, 
14.1, 14, 14, 14.3, 14.3, 14, 13.5, 13, 12.7, 12.6, 12.4, 12.5, 
12.4, 12.2, 11.8, 11.6, NA), `15-17 years` = c(40.7, 43.9, 38.8, 
32.5, 32, 32.3, 31.8, 31, 31, 30.5, 31.7, 33.6, 36.4, 37.5, 38.6, 
37.6, 37.5, 37.2, 35.5, 33.3, 31.4, 29.9, 28.2, 26.9, 24.5, 23.1, 
22.2, 21.8, 21.1, 21.6, 21.7, 21.1, 19.6, 17.3, 15.4, 14.1, 12.3, 
10.9, 9.9, 8.8, 7.9, 7.2, NA), `18-19 years` = c(132.7, 166.7, 
114.7, 82.1, 80, 79.4, 77.4, 77.4, 79.6, 79.6, 78.5, 79.9, 84.2, 
88.6, 94, 93.6, 91.1, 90.2, 87.7, 84.7, 82.1, 80.9, 79, 78.1, 
75.5, 72.2, 69.6, 68.7, 68.4, 71.2, 71.7, 68.2, 64, 58.2, 54.1, 
51.4, 47.1, 43.8, 40.7, 37.5, 35.1, 32.3, NA), `20–24 years` = c(196.6, 
258.1, 167.8, 115.1, 112.2, 111.6, 107.8, 106.8, 108.3, 107.4, 
107.9, 110.2, 113.8, 116.5, 115.3, 113.7, 111.3, 109.2, 107.5, 
107.8, 107.3, 108.4, 107.9, 109.7, 105.6, 103.1, 102.3, 101.5, 
101.8, 105.5, 105.4, 101.8, 96.2, 90, 85.3, 83.1, 80.7, 79, 76.8, 
73.8, 71, 68, NA), `25–29 years` = c(166.1, 197.4, 145.1, 112.9, 
111.5, 111, 108.5, 108.7, 111, 109.8, 111.6, 114.4, 117.6, 120.2, 
117.2, 115.7, 113.2, 111, 108.8, 108.6, 108.3, 110.2, 111.2, 
113.5, 113.8, 114.7, 116.7, 116.5, 116.5, 118, 118.1, 115, 111.5, 
108.3, 107.2, 106.5, 105.5, 105.8, 104.3, 102.1, 98, 95.3, NA
), `30–34 years` = c(103.7, 112.7, 73.3, 61.9, 61.4, 64.1, 
64.9, 67, 69.1, 70.1, 72.1, 74.8, 77.4, 80.8, 79.2, 79.6, 79.9, 
80.4, 81.1, 82.1, 83, 85.2, 87.1, 91.2, 91.8, 92.6, 95.7, 96.2, 
96.7, 98.9, 100.6, 99.4, 97.5, 96.5, 96.5, 97.3, 98, 100.8, 101.5, 
102.7, 100.3, 99.7, NA), `35–39 years` = c(52.9, 56.2, 31.7, 
19.8, 20, 21.2, 22, 22.9, 24, 24.4, 26.3, 28.1, 29.9, 31.7, 31.9, 
32.3, 32.7, 33.4, 34, 34.9, 35.7, 36.9, 37.8, 39.7, 40.5, 41.6, 
43.9, 45.5, 46.4, 47.5, 47.6, 46.8, 46.1, 45.9, 47.2, 48.3, 49.3, 
51, 51.8, 52.7, 52.3, 52.6, NA), `40–44 years` = c(15.1, 15.5, 
8.1, 3.9, 3.8, 3.9, 3.9, 3.9, 4, 4.1, 4.4, 4.8, 5.2, 5.5, 5.5, 
5.9, 6.1, 6.4, 6.6, 6.8, 7.1, 7.4, 7.4, 8, 8.1, 8.3, 8.7, 9, 
9.1, 9.4, 9.6, 9.9, 10, 10.2, 10.3, 10.4, 10.4, 10.6, 11, 11.4, 
11.6, 11.8, NA), `45-54 years` = c(1.2, 0.9, 0.5, 0.2, 0.2, 0.2, 
0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.3, 0.3, 0.3, 0.3, 
0.3, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5, 0.5, 0.5, 0.6, 0.6, 0.6, 0.7, 
0.7, 0.7, 0.7, 0.7, 0.8, 0.8, 0.8, 0.9, 0.9, 0.9, NA)), class = c("spec_tbl_df", 
"tbl_df", "tbl", "data.frame"), row.names = c(NA, -43L), spec = structure(list(
    cols = list(Year = structure(list(), class = c("collector_double", 
    "collector")), `Crude Birth Rate` = structure(list(), class = c("collector_double", 
    "collector")), `15-17 years` = structure(list(), class = c("collector_double", 
    "collector")), `18-19 years` = structure(list(), class = c("collector_double", 
    "collector")), `20–24 years` = structure(list(), class = c("collector_double", 
    "collector")), `25–29 years` = structure(list(), class = c("collector_double", 
    "collector")), `30–34 years` = structure(list(), class = c("collector_double", 
    "collector")), `35–39 years` = structure(list(), class = c("collector_double", 
    "collector")), `40–44 years` = structure(list(), class = c("collector_double", 
    "collector")), `45-54 years` = structure(list(), class = c("collector_double", 
    "collector"))), default = structure(list(), class = c("collector_guess", 
    "collector")), skip = 1), class = "col_spec"))

CodePudding user response：

That R for Data Science book that was recommended by Johan Rosa is really good and you should definitely check out that chapter.

On another note, I looked at your data set and I'm wondering about more extreme values before 1980. I'm wondering if you might want to consider using a robust estimator in this case. Just a thought!

CodePudding user response：

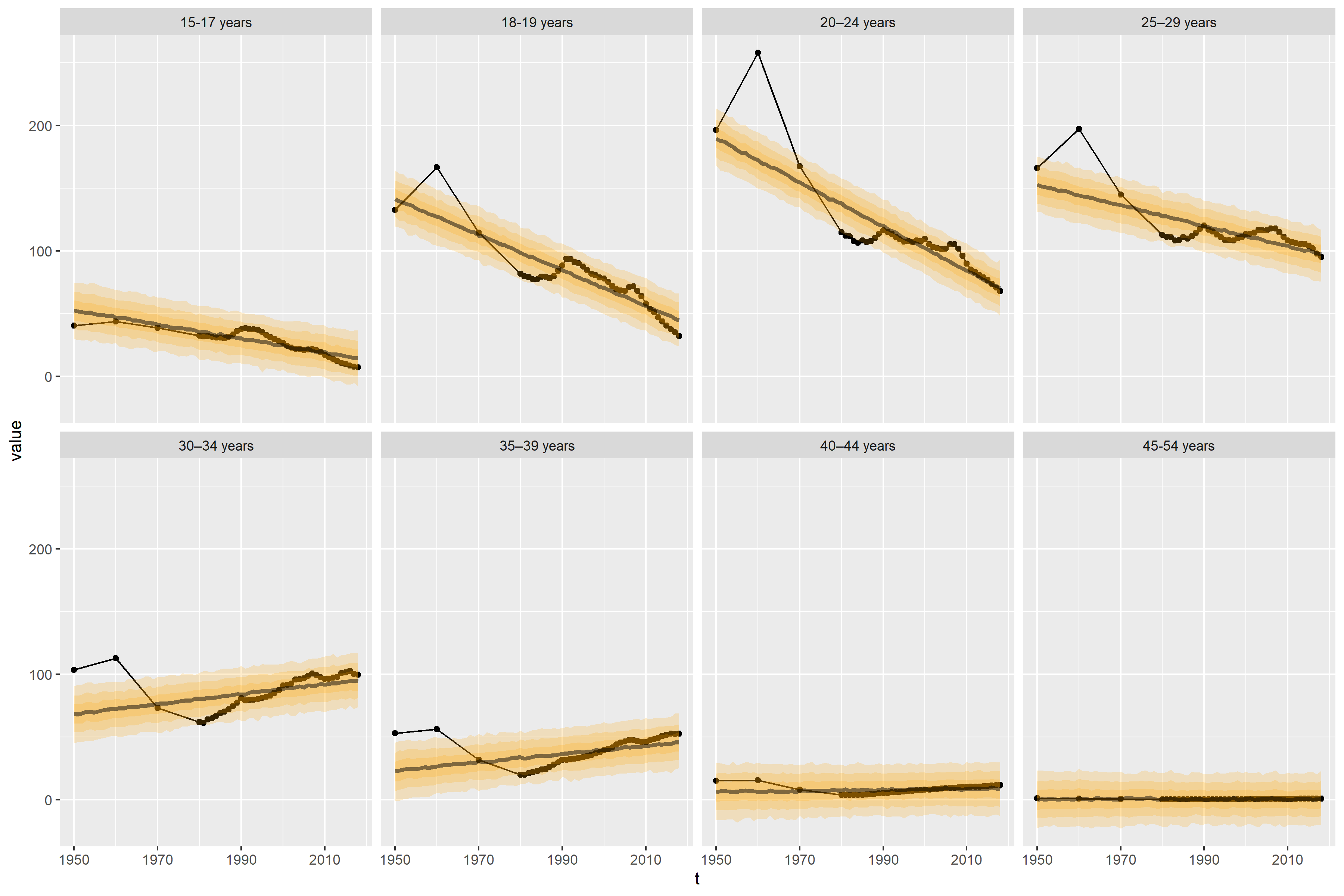
Bypassing a discussion on the suitability of a linear regression model for characterising birth rates, I'd probably start with a generalised linear mixed-effect model (treating the age band as the random effect).

First, let's reshape the data (I assume the original data is in data): Remove column "Crude Birth Rate", reshape from wide to long, and transform "Year" to time (in years) since min(data$Year).

df <- data %>%
    filter(!is.na(Year)) %>%
    select(-`Crude Birth Rate`) %>%
    pivot_longer(-Year) %>%
    mutate(t = Year - min(Year))

We can then fit the model (I'm using the Bayesian/rstan "version" of glmer). Here I am assuming normally distributed errors (which is not going to be correct, seeing that you are modelling birth rates, but will do for demonstration purposes).

library(rstanarm)
fit <- stan_glmer(
    value ~ 1   t   (1   t | name), 
    data = df)

Skipping model validation (which you shouldn't;-) we can visualise draws from the posterior predictive

library(tidybayes)
df %>%
    modelr::data_grid(
        name = unique(name),
        t = seq(min(t), max(t), by = 1)) %>%
    add_predicted_draws(fit) %>%
    ggplot(aes(t, value))   
    geom_point(data = df)   
    geom_line(data = df)   
    stat_lineribbon(aes(y = .prediction), fill = "orange", alpha = 0.2)  
    facet_wrap(~ name, ncol = 4)  
    scale_x_continuous(labels = ~ .x   min(df$Year))