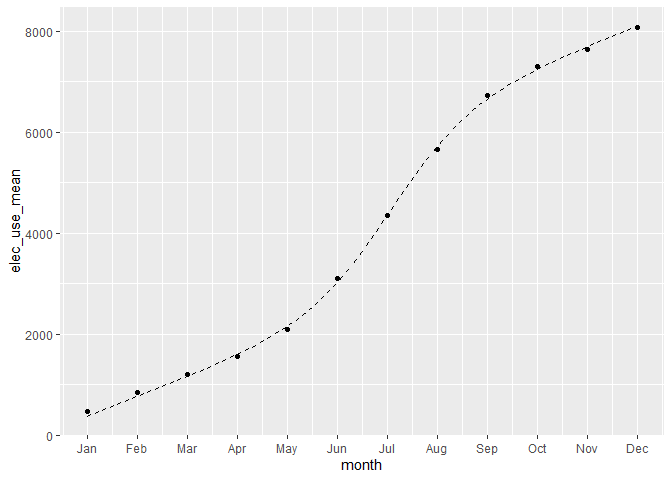
R: fitting a sigmoidal curve?-CodePudding

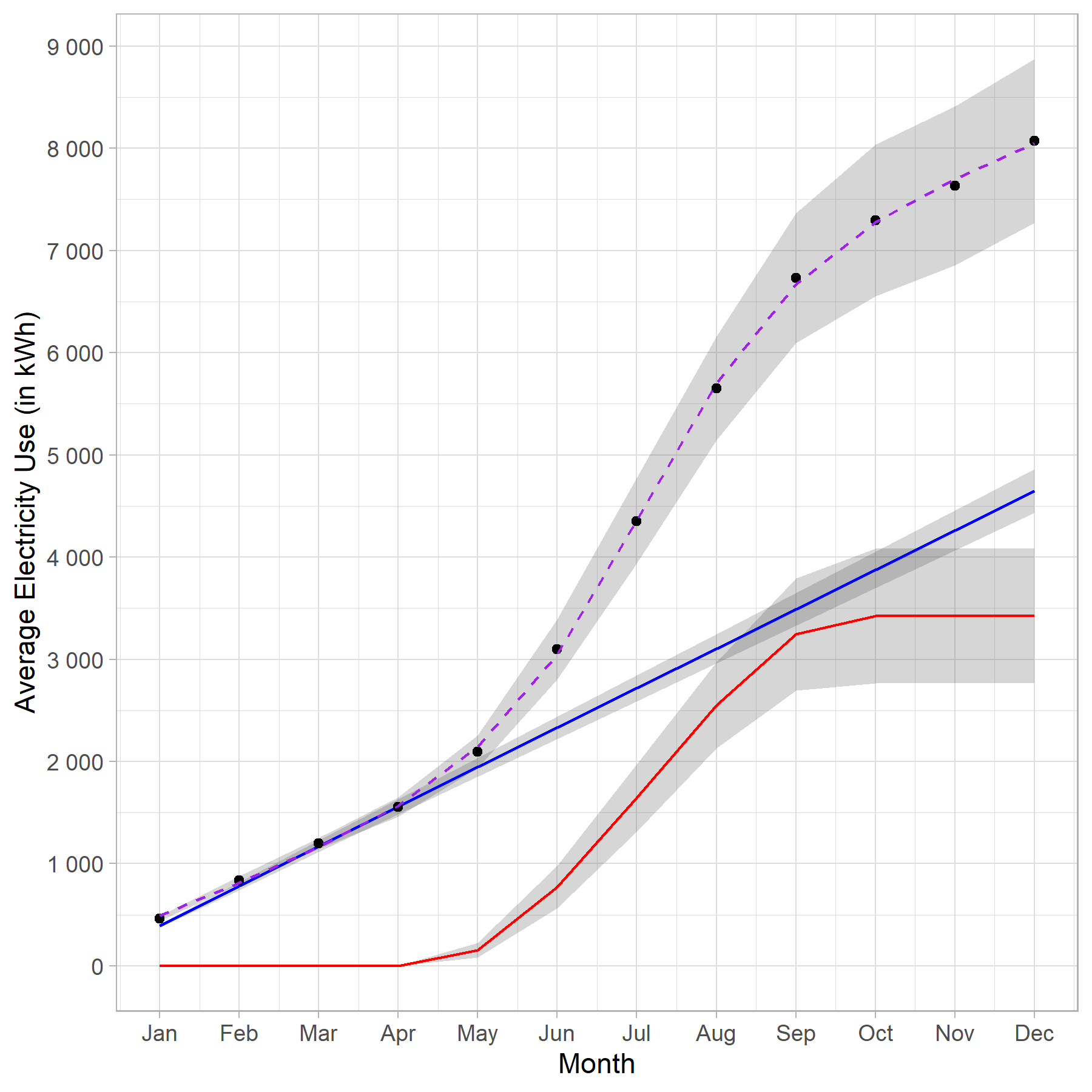
I was doing some analysis of my power bill and was trying to extract how much the air conditioning unit is using. By assuming that "normal" power use is fairly constant over the year and that the A/C is only on during the hotter months, I was able to estimate some separation.

In the figure there are two lines:

the linear showing "normal use", cumulative
the sigmoidal showing AC use, cumulative

In trying to fit a good model through this total cumulative use, the nls function in R gave the dreaded singular gradient matrix at initial parameter estimates. Using different software (JMP) I could get good initial parameters, which are reflected in the purple fit curve.

Any idea how I can use R to get parameter estimates without the error?

nls model

nls(elec_use_mean ~ b0   b1 * month   a1 / (a2   a3 * exp(a4 * month)),
    start = list(b0 = 100, b1 = 310, a1 = 1300, a2 = 0.3, a3 = 600, a4 = -1.2),
    data = cumulative
    )


Error in nlsModel(formula, mf, start, wts, scaleOffset = scOff, nDcentral = nDcntr) : 
  singular gradient matrix at initial parameter estimates

Data:

month,elec_use_mean
1,461.46
2,839.46
3,1197.92
4,1553.59
5,2093.34
6,3096.42
7,4353.67
8,5652.51
9,6729.84
10,7296.92
11,7634.34
12,8071.84

Below is a picture

CodePudding user response：

An alternative way to parameterize a sigmoid curve is to use tanh, which can produce a nice converging model with only 4 parameters rather than 6. The formula can also be written in such a way as to allow the parameters to have clear meanings that lend themselves to close initial estimates:

elec_use_mean ~ b1 * month   6 * b0 * (1   tanh(a1 * (month - a0)))

where:

b0 is the average monthly air conditioner spend over the year
b1 is the average monthly background electricity spend over the year
a0 is the month of the year when air conditioner use is highest
a1 is a measure of how "seasonal" air con use is, where 0 is not seasonal at all (each month uses 1/12 of the air con total), and 1 means about 76% of air con use is in the two hottest months.

model <- nls(elec_use_mean ~ b1 * month   6 * b0 * (1   tanh(a1 * (month - a0))),
    start = list(b0 = 330, b1 = 300, a0 = 7, a1 = 0.5),
    data = cumulative
    )

summary(model)
#> 
#> Formula: elec_use_mean ~ b1 * month   6 * b0 * (1   tanh(a1 * (month - 
#>     a0)))
#> 
#> Parameters:
#>     Estimate Std. Error t value Pr(>|t|)    
#> b0 294.99540   16.88446   17.47 1.18e-07 ***
#> b1 379.93397   16.34690   23.24 1.25e-08 ***
#> a0   7.07014    0.05877  120.31 2.55e-14 ***
#> a1   0.61313    0.05616   10.92 4.39e-06 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 70.82 on 8 degrees of freedom
#> 
#> Number of iterations to convergence: 8 
#> Achieved convergence tolerance: 2.64e-06

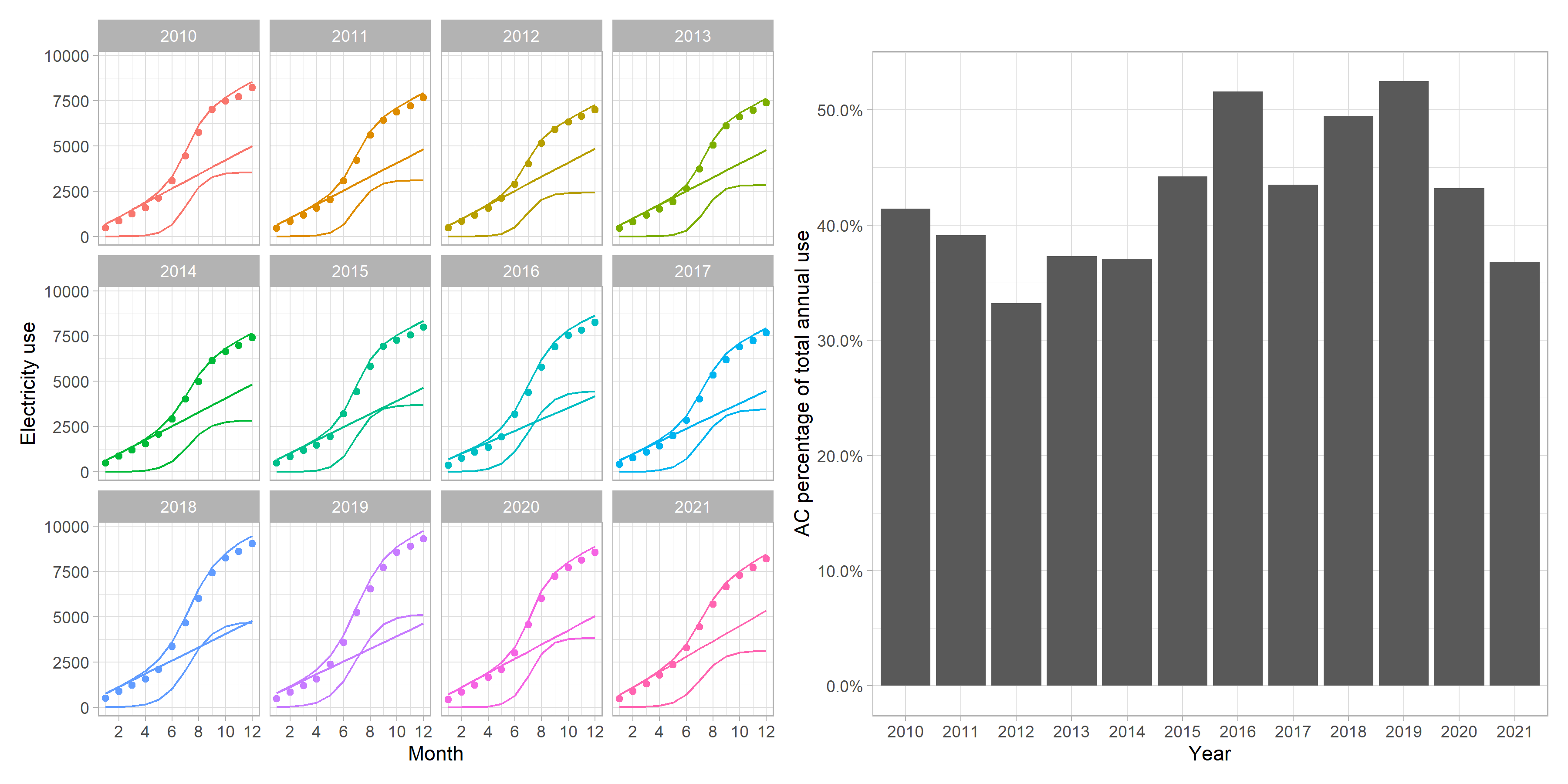
and we can see this fits well by generating a smooth set of predictions:

library(ggplot2)

new_df <- data.frame(month = seq(1, 12, 0.1))
new_df$elec_use_mean <- predict(model, new_df)

ggplot(cumulative, aes(month, elec_use_mean))  
  geom_point()  
  geom_line(data = new_df, linetype = 2)  
  scale_x_continuous(breaks = 1:12, labels = month.abb)

^{Created on 2022-04-21 by the}