As a software developer for geometry algorithms I ran into the following problem a few times already never really satisfies with how I solved it.

The problem statement

Imagine dominos in the 3D-cartesian space with the faces holding 3D-coordinates (x, y, z). An additional condition to this game is, that each coordinate exists only once in the game and is written on exactely the faces of two stones. A pair of dominos is found once one finds a matching pair of faces. A path is defined as an ordered list of dominos where each two pairwise adjacent elements (dominos) in the list form a match. There can be multiple paths in one game of domino.

Examples

An example would look as follows before and after playing the sorting game:

Game 1: Single path as an outcome.

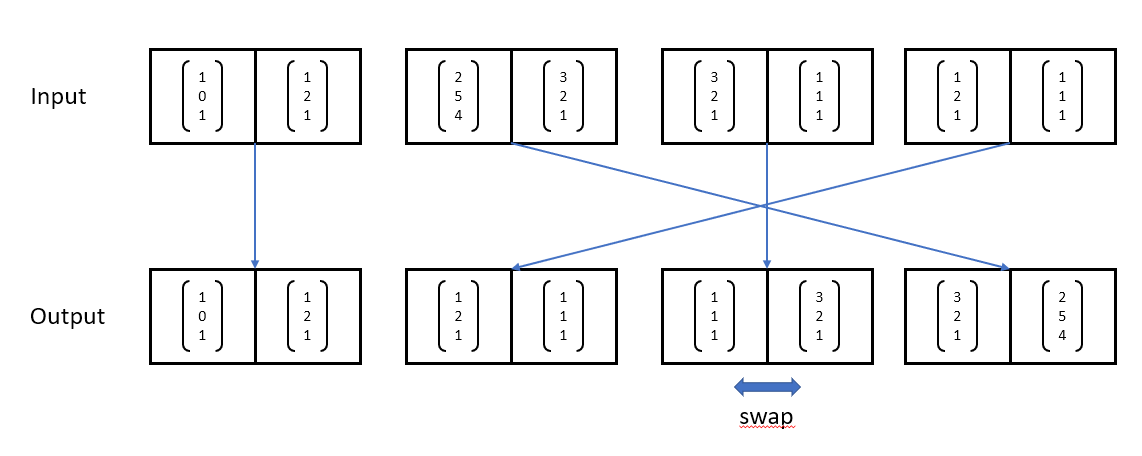
Game 2: Multiple paths as an outcome.

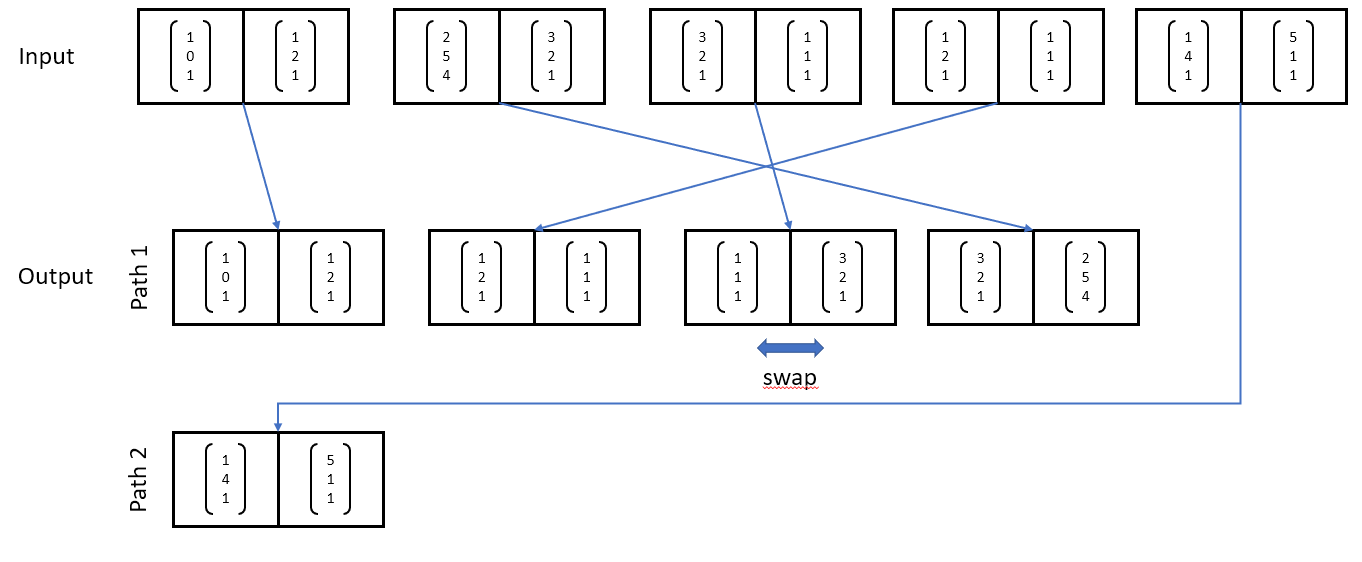
Is there a a) efficient and b) elegant solution to this problem?

Naive solution with while-loop

My best guess is something as follows:

Let the input list of dominos be called list.
Let the currently forming path be an ordered list called cur_path.
Let the resulting list of paths be called results.

While (list is not empty)
  If (cur_path is empty)
    Draw random piece of domino from list and put into cur_path.
    Continue
  Else
    // Search equals finding a match for open ends of cur_path,
    // i.e. the first and the last domino in cur_path.
    Search in list for matching domino
    If (Found matching domino)
      Draw found piece from list and put at correct position into cur_path
    Else
      // We have not found a match amongst all residual dominos.
      // Store current path into result paths and begin new.
      Store cur_path in results.
      Clear variable cur_path.
      Continue

return results

You will see that I while-loop over all elements in approx. O(n²). There are two approaches to this solution that I do not like. First, I do not like while-loops as they are always bound on conditions which does not feel deterministic. Second, I dont like how I neglect the geometric information of the dominos to narrow down the search space for matches. Do you think a sorted hierarchy like a bounding-volume hierarchy approach would be too overkill to solve this?

CodePudding user response：

This is solvable in O(n).

Here is untested Python:

    tiles_at = {} # will map coordinates to tiles.
    for tile in all_tiles:
        for face in tile.faces:
            if face not in tiles_at:
                tiles_at[face] = [tile]
            else:
                tiles_at[face].append(tile)

    is_used = set() # will hold the used tiles
    paths = [] # will hold the final answer. Does not find loops.
    for face, tiles in tiles_at.items():
        if 1 == len(tiles) and tiles[0] not in is_used:
            # Found the start of a path.
            is_used.add(tiles[0])
            last_face = face
            last_tile = tiles[0]
            if face != tiles[0].faces[0]:
                last_tile = last_tile.flip()
            path = [last_tile]

            # Find the path
            while True:
                # Find the unused face.
                last_face = last_tile.faces[1]

                # Find the next tile in the path, if any.
                if 1 == len(tiles_at[last_face]):
                    break # EXIT LOOP AT END OF PATH
                elif last_tile == tiles_at[last_face][0]:
                    last_tile = tiles_at[last_face][1]
                else:
                    last_tile = tiles_at[last_face][0]
                # We used this tile
                is_used.add(last_tile)
                if last_face == last_tile.faces[1]:
                    last_tile = last_tile.flip()
                path.append(last_tile)
        # and record the path
        paths.append(path)

The idea is a O(n) scan to add all faces of tiles to a hash. An O(n) scan to find all possible starting points, and for each starting point a scan of the path that will, over all paths, visit every one of O(n) tiles exactly once.

Which, combined, is O(n).