Numerically finding first derivative of non-uniform 2D data-CodePudding

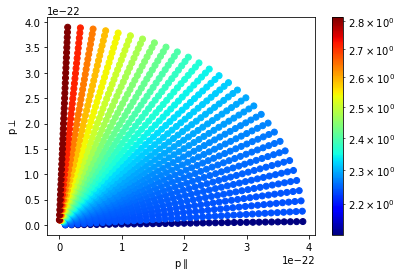
I initially have 2 arrays p and angle, and plug them into an equation fh to get a third array z. After I get this data, I change the arrays p and angle into p_perpendicular and p_parallel, where p_perpendicular = p* sin(angle) and p_parallel = p*cos(angle).

import numpy as np 
import matplotlib.pyplot as plt
import matplotlib.colors as colors
from numpy import histogram2d

def func(p,alpha):
   fh = (1/((1 ((p**(1/2))))**(3/2)))*(1-np.tanh((np.cos(alpha*np.pi/180))**(1/2)) (1 np.tanh(alpha)**(1/2)))
return (fh)

p=[]
angle=[]
z=[]
for p_loop in np.arange(1e-23,4e-22,1e-23): 
    for alpha in np.arange(1,90,3): 
        p.append(p_loop)
        angle.append(alpha)
        z.append(func(p_loop,alpha))

p_parallel = (np.array(p)*np.cos(np.array(angle)*np.pi/180))   #array of parallel p
p_perpendicular = (np.array(p)*np.sin(np.array(angle)*np.pi/180))  #array of perpendicular p

I know that I can find an approximate derivative of dz/dp and dz/d(angle) from the initial data, but am not sure how to find the derivative of dz/dp_parallel or dz/dp_perpendicular.

My first idea was binning with 2d histogram, but that resulted in large inaccuracies. Is there some interpolation method or polar binning method or other method that would be best to have the data in p_parallel and p_perpendicular space?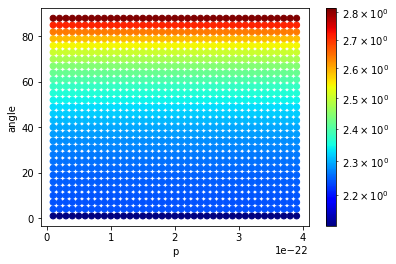

CodePudding user response：

You have performed change of variables. From the chain rule:

  dz/dp = dz/dp_par dp_par/dp   dz/dp_perp dp_perp/dp
  dz/dangle = dz/dp_par dp_par/dangle   dz/dp_perp dp_perp/dangle

Given your transformation:

# the Jacobian of polar coordinates with respect to cartesian
# both `p` and `angle` are numpy arrays
J = np.array(
    [
        [np.cos(angle * np.pi / 180), -np.pi * p * np.sin(angle * np.pi / 180) / 180],
        [np.sin(angle * np.pi / 180), np.pi * p * np.cos(angle * np.pi / 180) / 180],
    ]
)

# J.shape = (2, 2, 1170).
# Transpose it such that the longest dim is first
J = np.transpose(J, axes=(2, 0, 1))

dz = <<your approximation of derivative [dz/dp, dz/dangle]>>
# dz.shape = (1170, 2)

Then the approximation to dz/dp_par, dz/dp_perp is given by solving

np.linalg.solve(J, dz)