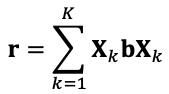Given a 3d array X with dimensions (K,n,m) that can be considered as a stack of K (n,m) matrices and a 1d vector b (dim n), the goal is to obtain the resulting vector r (dim n) each component of which is calculated as:

It is easy to see that the expression under the k-summation (i.e. two internal sums) is just a dot product X_k b X_k (and, therefore, can easily be calculated using numpy). So, the desired vector r is

where X_k is the k-th 2d (n,m) 'layer' of 3d array X.

I.e. the current solution is

r = 0
for k in range(K):
    r  = x[k,:,:] @ (b @ x[k, :, :])

Can r be efficiently calculated avoiding a for-loop by k? Or maybe there is another efficient way to calculate r?

(I tried np.tensordot but since it is just pure summation by k I didn't get a correct result yet.)

CodePudding user response：

This looks like a perfect usecase for einsum:

r = np.einsum('kij,l,klj->i', x, b, x)

which will vectorize the operation, e.g. it's more optimal than a for loop.