I can not figure out why my for loop is not being taken in MATLAB-CodePudding

In MATLAB, I am trying to write a program that will take 3 coordinates on a graph, (x,y), use those values to solve a system of equations that will find the coefficients of a polynomial equation, y = ax^2 bx c, which I can then use to plot a parabola.

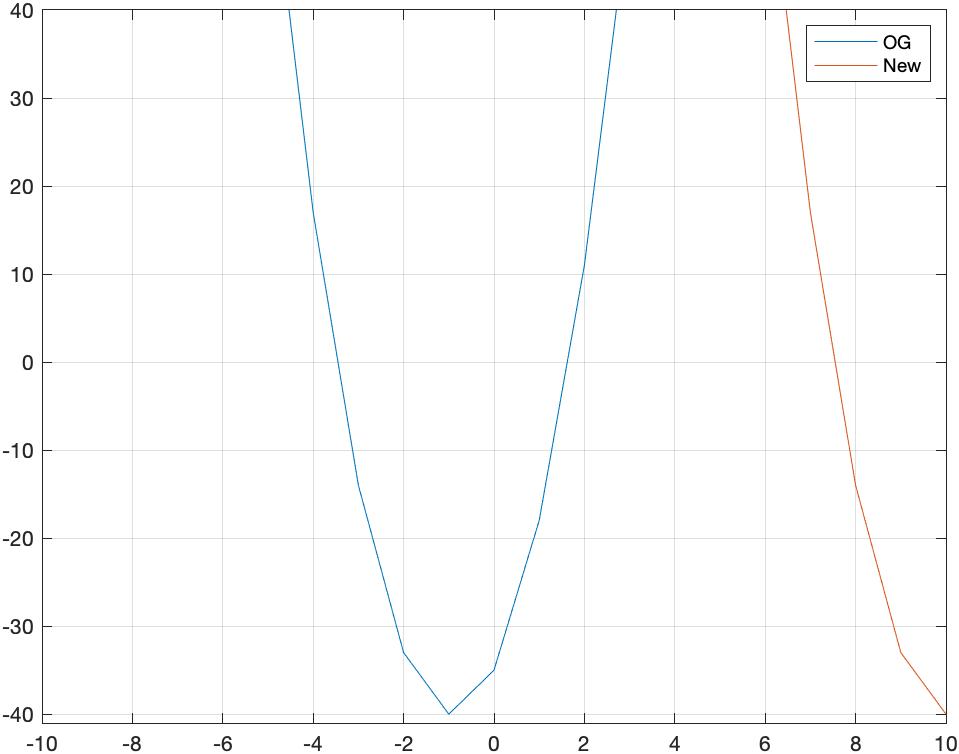
To test my code, I figured I could start with a polynomial, graph it, find the minimum location of the parabola, use its immediate neighbors for my other 2 locations, then run those 3 locations through my code which should spit out the coefficients of my original polynomial. But for some reason, my resulting parabola is right shifted and my values for b and c are incorrect.

Does anyone see where my issue is? I am out of ideas

clear all; close all;

x = -10:10;

%Original Polynomial
y = 6.*x.^2   11.*x -35;

% Find 3 Locations
[max_n, max_i] = min(y)
max_il = max_i - 1                 % left neighbor of max_ni
max_nl = y(max_il)                 % value at max_il
max_ir = max_i   1                 % left neighbor of max_ni
max_nr = y(max_ir)                 % value at max_ir

% Solve for coefficients
syms a b c
equ = (a)*(max_i)^2   (b)*(max_i)   (c) == (max_n);
equ_l = (a)*(max_il)^2   (b)*(max_il)   (c) == (max_nl);
equ_r = (a)*(max_ir)^2   (b)*(max_ir)   (c) == (max_nr);

sol = solve([equ, equ_l, equ_r],[a, b, c]);

Sola = sol.a
Solb = sol.b
Solc = sol.c

% New Polynomial
p = (sol.a).*(x).^2   (sol.b).*(x)  (sol.c);


%Plot
plot(x,y); grid on; hold on;
plot(x, p); 
axis([-10 10 -41 40])
[max_np, max_ip] = min(p)
legend('OG', 'New')

plot

CodePudding user response：

You are confusing the index into your array y, and the corresponding x coordinate.

x = -10:10;
y = 6.*x.^2   11.*x -35;

[max_n, max_i] = min(y)

Here. max_i is the index into the y array, the corresponding x coordinate would be x(max_i).

I suggest you find three data points to fit your curve to as follows:

[~, max_i] = min(y);
pts_x = x(max_i   (-1:1));
pts_y = y(max_i   (-1:1));

then use pts_x(i) and pts_y(i) as your x and y values:

syms a b c
equ = a * pts_x.^2   b * pts_x   c == pts_y;
sol = solve(equ, [a, b, c]);