Calculate Decay Rate in Python-CodePudding

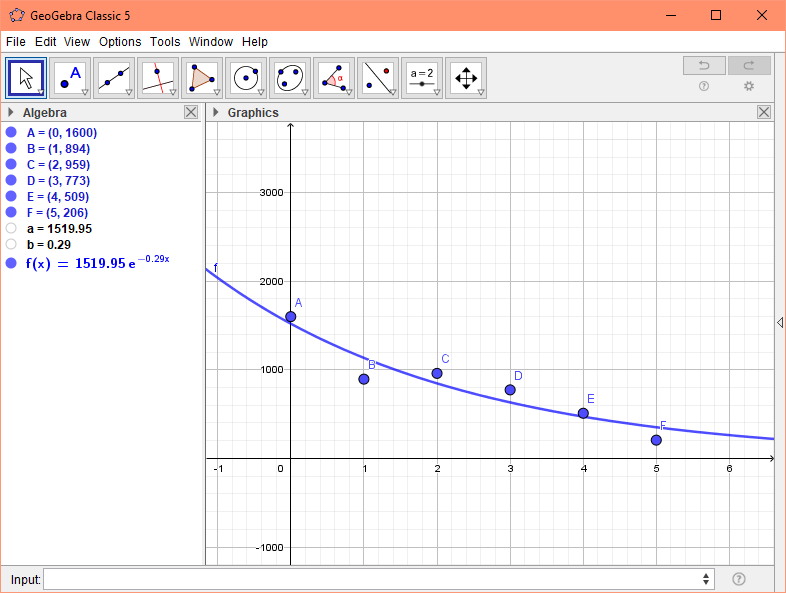
I have dataset which somewhat follows an exponentional decay

df_A
Period  Count
0       1600
1       894
2       959
3       773
4       509
5       206

I want to calculate the decay rate by using 2 methods as I'm expecting both to give the same result, however, I get different results?

This is the first method:

decay_rate1 = (10**(log(df_A['Count'].iloc[5]/df_A['Count'].iloc[0]) / 5)) - 1

This is the second method:

decay_rate2 = np.log(df_A['Count'].iloc[0])/log(df_A['Count'].iloc[5]

What is the correct method of calculating the decay rate of a dataset?

CodePudding user response：

Not sure what you mean by "over-complicated". Can you explain your 2 methods? I'm not sure I follow how you arrived by them? In any case, scipy.optimize.curve_fit does all the heavy lifting for you:

import numpy as np
import pandas as pd
from scipy.optimize import curve_fit


def f(t, a, b):
    return a * np.exp(-b * t)


(a, b), *_ = curve_fit(f, df.Period, df.Count)

Result:

In [4]: a
Out[4]: 1519.9510695102867

In [5]: b
Out[5]: 0.29266498021489273

Note that due to your data having quite large values, you'll actually get a RunTimeWarning, so you can scale your df.Count column and still get the decay rate, b:

(a, b), *_ = curve_fit(f, df.Period, df.Count / df.Count.max())

Output:

In [6]: a
Out[6]: 0.9499694152031338

In [7]: b
Out[7]: 0.29266497643362804

You can also recover the true a by multiplying by df.Count.max():

In [8]: a * df.Count.max()
Out[8]: 1519.9510643250142