What is the equation for SVR inference using an RBF kernel?-CodePudding

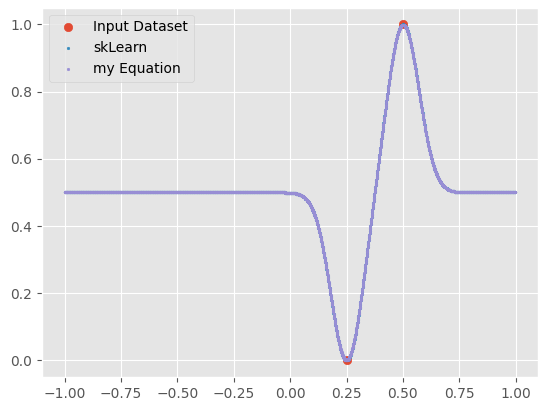
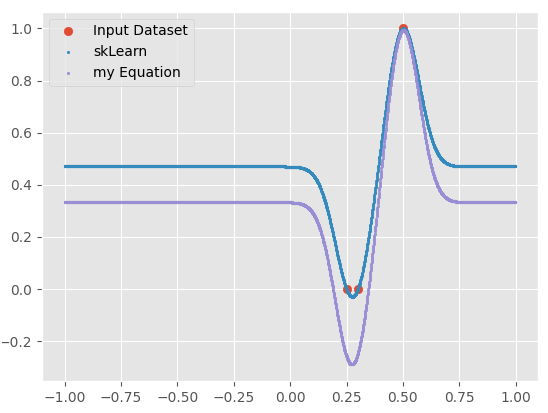
I'm using sklearn for SVR (regression) using an RBF kernel. I'm want to know how the inference is done under the hood. I thought it was a function of the support vectors, function mean, and gamma, but it appears I'm missing one aspect (probably some scaling based on how close 2 points are.

Here is "my Equation" that I've tried in the graph's below.

out = mean
for vect in vectors:
    out = out   (vect.y - mean) * math.exp(-(vect.x - x) ** 2 * gamma)

When I do just 2 points spaced away, my equation matches what skLearn reports with svr.predict.

With 3 training points and 2 close together, my equation does not match what svr.predict gives:

Given the support vectors, gamma, and mean, and anything else needed, what is the equation for SVR inference with RBF kernel? Can those be obtained from the sklearn svr class?

CodePudding user response：

The equation that works for me using sklearn library and SVR inference with RBF kernel is as follows with python code:

# x and y is already defined, and is the training data for the SVR
svr = svm.SVR(kernel="rbf", C=C, gamma=gamma, epsilon=epsilon, tol=tol)
svr.fit(x,y)
vectors = []
for i in svr.support_:
    vectors.append([x[i][0], y[i]])
out = svr._intercept_[0]
for vect, coef in zip(vectors, svr._dual_coef_[0]):
    out = out   coef * math.exp(-(vect[0] - x) ** 2 * gamma)

I found that svr._intercept_[0] contains the y offset for the function.

I found that svr._dual_coef_[0] contains the coefficients to multiply each of the exponentials by.

I found that svr.support_ contains the indexes of the elements in your training set used as the support vectors.

I realize I'm accessing what is intended to be accessed within the svr class only, however, I don't see an official API method for accessing these variables, and this is working for me for now.