I am trying to integrate orbits of stars using a Velocity-Verlet integrator inside a potential. However, my current algorithm takes around 25 seconds per orbit, I aim to integrate around 1000 orbits which would take around 7 hours. Therefore I hope someone can help me to optimize the algorithm:
The Velocity-Verlet integrator is defined as (see verlet_integration() for an implementation):
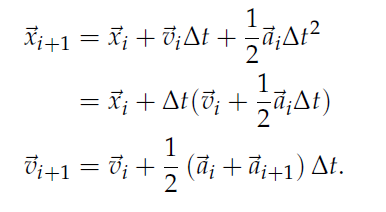
I want to integrate orbits using a Simple Logarithmic Potential (SLP) defined as:
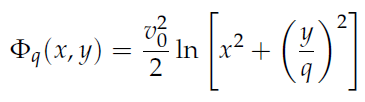
The value v_0 is always equal to 1 and the value q can either be 0.7 or 0.9 (see SLP()).
By using this potential, the acceleration can be calculated which is necessary for this integrator (see apply_forces())
After this I choose x = 0 as a starting value for all orbits, and the energy E = 0 as well. Using that starting values for vx can be calculated (see calc_vx())
To have orbits that are accurate enough, the time step needs to be 1E-4 or smaller. I need to analyze these orbits later, for that they need to be sufficiently long enough, thus I integrate between t=0 and t=200.
I need to calculate values for the entire allowed phase space of (y, vy). The allowed phase space is where the method calc_vx() doesn't result in a square root of a negative number. Thus for that a large number of orbits need to be integrated. I hope to be able to calculate at least 1000 values. But 10,000 would definitively be more ideal. Although maybe that's asking for too much.
If you have any ideas for performance improvements, please let me know. Using another language is not an option, so please don't suggest that.
An example of how these orbits look can be seen here:
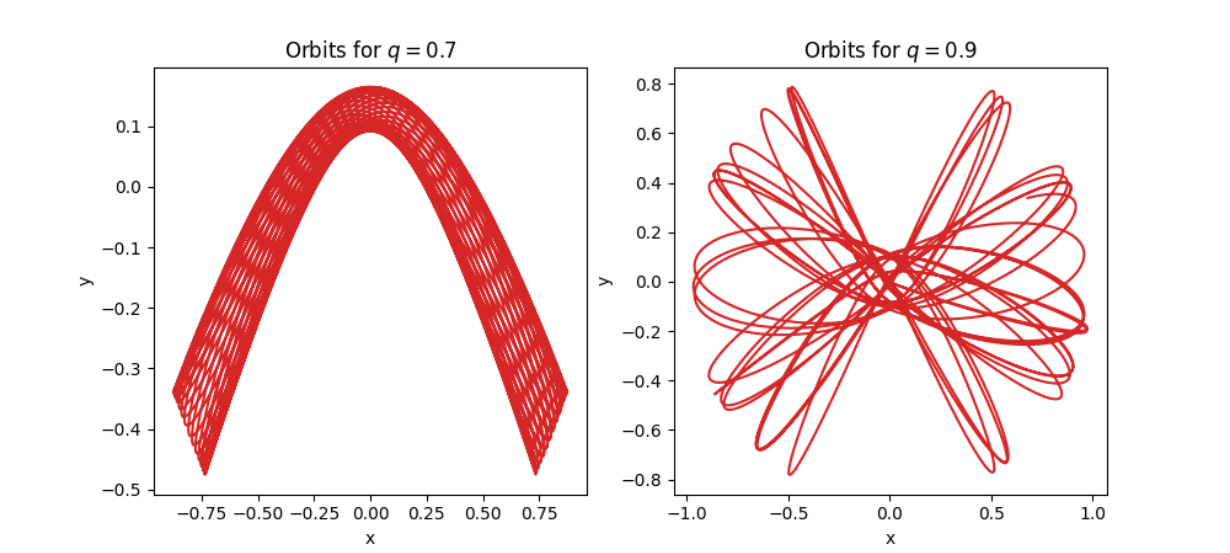
Everything necessary to run the code should be found below, as well as starting values to run it.
UPDATE: I have implemented the suggestions by mivkov, this reduced the time to 9 seconds, 3 seconds faster, but it's still quite slow. Any other suggestions are still welcome
import numpy as np
def calc_vx(y, vy, q):
"""
Calculate starting value of x velocity
"""
vx2 = -np.log((y / q) ** 2) - vy ** 2
return np.sqrt(vx2)
def apply_forces(x, y, q):
"""
Apply forces to determine the accelerations
"""
Fx = -x / (y ** 2 / q ** 2 x ** 2)
Fy = -y / (q ** 2 * x ** 2 y ** 2)
return Fx, Fy
def verlet_integration(start, dt, steps, q):
# initialise an array and set the first value to the starting value
vals = np.zeros((steps, *np.shape(start)))
vals[0] = start
# run through all elements and apply the integrator to each value
for i in range(steps - 1):
x_vec, v_vec, a_vec = vals[i]
new_x_vec = x_vec dt * (v_vec 0.5 * a_vec * dt)
new_a_vec = apply_forces(*new_x_vec, q)
new_v_vec = v_vec 0.5 * (a_vec new_a_vec) * dt
vals[i 1] = new_x_vec, new_v_vec, new_a_vec
# I return vals.T so i can use the following to get arrays for the position, velocity and acceleration
# ((x, vx, ax), (y, vy, ay)) = verlet_integration_vec( ... )
return vals.T
def integration(y, vy, dt, t0, t1, q):
# calculate the starting values
vx = calc_vx(y, vy, q)
ax, ay = apply_forces(0, y, q)
start = [(0, y), (vx, vy), (ax, ay)]
steps = round((t1 - t0) / dt) # bereken het aantal benodigde stappen
e = verlet_integration(start, dt, steps, q) # integreer
return e
((x, vx, ax), (y, vy, ay)) = integration(0.1, 0.2, 1E-4, 0, 100, 0.7)
CodePudding user response:
I see two things which can help here.
(1) Consider using an ODE solver from a library instead of the Verlet method which you wrote by hand. Runge-Kutta methods and variations on that (e.g. Runge-Kutta-Fehlberg) are widely applicable, I'd try that first. It is likely that a library method will be written in C code, and therefore much faster, and also someone has already worked out the bugs. Both aspects will be useful for this problem.
(2) If you are required to write the ODE solver yourself, an idea to speed up the implementation in Python is to vectorize over trajectories so that you can make use of Numpy array operations. That is, create an array which represents all 1000 or 10,000 trajectories, and then advance all trajectories one step at a time. I am assuming you can rewrite the equations of motion in matrix form.
As an aside, my advice is to keep the solution you have already worked out, since it seems to be working, and start on a separate implementation using ideas (1) or (2), and use your original implementation to verify the results.
CodePudding user response:
The first thing to do is to use a profiler to analyse the hotspots in your code. You can use cProfile.run to do that. A basic report shows that nearly all the time is spent in the functions: x_func, v_func and apply_forces (called 200_000 times):
ncalls tottime percall cumtime percall filename:lineno(function)
200000 0.496 0.000 0.496 0.000 apply_forces
199999 0.279 0.000 2.833 0.000 func_verlet
199999 0.713 0.000 0.713 0.000 x_func
199999 0.780 0.000 0.780 0.000 v_func
1 0.000 0.000 0.000 0.000 SLP
199999 0.222 0.000 0.718 0.000 a_func
1 0.446 0.446 3.279 3.279 verlet_integration
[...]
A quick analysis of x_func and v_func show that you are calling Numpy functions on tiny array. The thing is Numpy is not optimized to deal with such a small array (Numpy make many checks on the input that are expensive compared to the computation time on tiny arrays).
The main way to address this problem is to use vectorized Numpy calls operating on much bigger array. The thing is this solution require to completely redesign your code so to get ride of the for i in range(steps - 1) loop which is the root of the problem.
An alternative solution is to use Numba so to avoid the Numpy overhead. This solution is much simpler (though your teacher may not expect this if the goal is to learn Numpy). Here is an example:
import numpy as np
import numba as nb
@nb.njit
def SLP(x, y, v0, q):
return 0.5 * v0 ** 2 * np.log(x ** 2 (y / q) ** 2)
@nb.njit
def calc_vx(x, y, vy, q):
"""
Calculate starting value of x velocity
"""
vx2 = -2 * SLP(x, y, 1, q) - vy ** 2
return np.sqrt(vx2)
@nb.njit
def apply_forces(x, y, v0, q):
"""
Apply forces to determine the accelerations
"""
Fx = -(v0 ** 2 * x) / (y ** 2 / q ** 2 x ** 2)
Fy = -(v0 ** 2 * y) / (q ** 2 * x ** 2 y ** 2)
return np.array([Fx, Fy])
@nb.njit
def x_func(x_vec, v_vec, a_vec, dt):
return x_vec dt * (v_vec 0.5 * a_vec * dt)
@nb.njit
def v_func(v_vec, a_vec, new_a_vec, dt):
return v_vec 0.5 * (a_vec new_a_vec) * dt
@nb.njit
def a_func(x_vec, dt, q):
x, y = x_vec
return apply_forces(x, y, 1, q)
# The parameter is a signature of the function that provides the input type to
# Numba so it can eagerly compile the function and all the dependent functions.
# Please read the Numba documentation for more information about this.
@nb.njit('(float64[:], float64[:], float64[:], float64, float64)')
def func_verlet(x_vec, v_vec, a_vec, dt, q):
# calculate the new position, velocity and acceleration
new_x_vec = x_func(x_vec, v_vec, a_vec, dt)
new_a_vec = a_func(new_x_vec, dt, q)
new_v_vec = v_func(v_vec, a_vec, new_a_vec, dt)
out = np.empty((len(new_x_vec), 3))
out[:,0] = new_x_vec
out[:,1] = new_v_vec
out[:,2] = new_a_vec
return out
def verlet_integration(start, f, dt, steps, q):
# initialise an array and set the first value to the starting value
vals = np.zeros((steps, *np.shape(start)))
vals[0] = start
# run through all elements and apply the integrator to each value
for i in range(steps - 1):
vals[i 1] = f(*vals[i].T, dt, q)
# I return vals.T so i can use the following to get arrays for the position, velocity and acceleration
# ((x, y), (vx, vy), (ax, ay)) = verlet_integration_vec( ... )
return vals.T
def integration(y, vy, dt, t0, t1, q):
# calculate the starting values
x = 0
vx = calc_vx(x, y, vy, q)
ax, ay = apply_forces(x, y, 1, q)
start = [(x, vx, ax), (y, vy, ay)]
steps = round((t1 - t0) / dt) # calculate the number of necessary steps
return verlet_integration(start, func_verlet, dt, steps, q)
((x_, y_), (vx_, vy_), (ax_, ay_)) = integration(0.1, 0.2, 1E-4, 0, 20, 0.7)
Note that some function have been modified so to avoid the use of function/operators not supported by Numba. For example, the unary * operator to unwrap Numpy array or lists is unsupported but it is generally quite inefficient anyway.
The resulting code is 5 times faster.
The profiler now show that the function verlet_integration is responsible for a major part of the execution due to the overhead of the for loop (including the * operator and function calls). This part cannot easily be ported to Numba due to the lambda. I think it can be made twice faster if you succeed to redesign this part to avoid the lambda and the unwrapping. In fact, operating on array of 2 items is pretty inefficient, even with Numba. Operating on scalar will make the code a bit less readable but much faster (certainly both with and without Numba). I guess the code can be made several time faster again.
UPDATE: with the updated code, Numba can help much better since the main performance bottleneck is now fixed. Here is the new Numba version:
import numpy as np
import numba as nb
@nb.njit
def calc_vx(y, vy, q):
vx2 = -np.log((y / q) ** 2) - vy ** 2
return np.sqrt(vx2)
@nb.njit
def apply_forces(x, y, q):
Fx = -x / (y ** 2 / q ** 2 x ** 2)
Fy = -y / (q ** 2 * x ** 2 y ** 2)
return np.array([Fx, Fy])
@nb.njit('(float64[:,:], float64, int_, float64)')
def verlet_integration(start, dt, steps, q):
vals = np.zeros((steps, 3, 2))
vals[0] = start
for i in range(steps - 1):
x_vec, v_vec, a_vec = vals[i]
new_x_vec = x_vec dt * (v_vec 0.5 * a_vec * dt)
x, y = new_x_vec
new_a_vec = apply_forces(x, y, q)
new_v_vec = v_vec 0.5 * (a_vec new_a_vec) * dt
vals[i 1, 0] = new_x_vec
vals[i 1, 1] = new_v_vec
vals[i 1, 2] = new_a_vec
return vals.T
def integration(y, vy, dt, t0, t1, q):
vx = calc_vx(y, vy, q)
ax, ay = apply_forces(0, y, q)
start = [(0, y), (vx, vy), (ax, ay)]
steps = round((t1 - t0) / dt)
e = verlet_integration(np.array(start), dt, steps, q)
return e
((x, vx, ax), (y, vy, ay)) = integration(0.1, 0.2, 1E-4, 0, 100, 0.7) # 9.7
This is 36 times faster than the updated code of the question. It takes just 0.27 second on my machine as opposed to 9.7 for the initial code.
CodePudding user response:
Inlining apply_forces speeds up @JérômeRichard's solution by ~2x in my benchmarks.
import numpy as np
import numba as nb #tested with numba 0.55.2
@nb.njit
def calc_vx(y, vy, q):
vx2 = -np.log((y / q) ** 2) - vy ** 2
return np.sqrt(vx2)
@nb.njit
def verlet_integration(start, dt, steps, q):
vals = np.zeros((steps, 3, 2))
vals[0] = start
for i in range(steps - 1):
x_vec, v_vec, a_vec = vals[i]
x, y = x_vec dt * (v_vec 0.5 * a_vec * dt)
ax, ay = -x / (y ** 2 / q ** 2 x ** 2), -y / (q ** 2 * x ** 2 y ** 2)
vx, vy = v_vec[0] 0.5 * (a_vec[0] ax) * dt, v_vec[1] 0.5 * (a_vec[1] ay) * dt
vals[i 1, 0] = x, y
vals[i 1, 1] = vx, vy
vals[i 1, 2] = ax, ay
return vals.T
@nb.njit
def integration(y, vy, dt, t0, t1, q):
vx = calc_vx(y, vy, q)
ax, ay = 0, -y / y**2
start = np.array([[0, y], [vx, vy], [ax, ay]])
steps = round((t1 - t0) / dt)
return verlet_integration(start, dt, steps, q)
((x, vx, ax), (y, vy, ay)) = integration(0.1, 0.2, 1E-4, 0, 100, 0.7)
