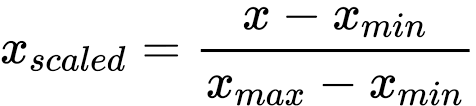How do I preprocess this data containing a single feature with different scales? This will then be used for supervised machine learning classification.
Data
import pandas as pd
import numpy as np
np.random.seed = 4
df_eur_jpy = pd.DataFrame({"value": np.random.default_rng().uniform(0.07, 3.85, 50)})
df_usd_cad = pd.DataFrame({"value": np.random.default_rng().uniform(0.0004, 0.02401, 50)})
df_usd_cad["ticker"] = "usd_cad"
df_eur_jpy["ticker"] = "eur_jpy"
df = pd.concat([df_eur_jpy,df_usd_cad],axis=0)
df.head(1)
value ticker
0 0.161666 eur_jpy
We can see the different tickers contain data with a different scale when looking at the max/min of this groupby:
df.groupby("ticker")["value"].agg(['min', 'max'])
min max
ticker
eur_jpy 0.079184 3.837519
usd_cad 0.000405 0.022673
I have many tickers in my real data and would like to combine all of these in the one feature (pandas column) and use with an estimator in sci-kit learn for supervised machine learning classification.
CodePudding user response:
If I Understand Carefully (IIUC), you can use the min-max scaling formula:
You can apply this formula to your dataframe with implemented sklearn.preprocessing.MinMaxScaler like below:
from sklearn.preprocessing import MinMaxScaler
df2 = df.pivot(columns='ticker', values='value')
# ticker eur_jpy usd_cad
# 0 3.204568 0.021455
# 1 1.144708 0.013810
# ...
# 48 1.906116 0.002058
# 49 1.136424 0.022451
df2[['min_max_scl_eur_jpy', 'min_max_scl_usd_cad']] = MinMaxScaler().fit_transform(df2[['eur_jpy', 'usd_cad']])
print(df2)
Output:
ticker eur_jpy usd_cad min_max_scl_eur_jpy min_max_scl_usd_cad
0 3.204568 0.021455 0.827982 0.896585
1 1.144708 0.013810 0.264398 0.567681
2 2.998154 0.004580 0.771507 0.170540
3 1.916517 0.003275 0.475567 0.114361
4 0.955089 0.009206 0.212517 0.369558
5 3.036463 0.019500 0.781988 0.812471
6 1.240505 0.006575 0.290608 0.256373
7 1.224260 0.020711 0.286163 0.864584
8 3.343022 0.020564 0.865864 0.858280
9 2.710383 0.023359 0.692771 0.978531
10 1.218328 0.008440 0.284540 0.336588
11 2.005472 0.022898 0.499906 0.958704
12 2.056680 0.016429 0.513916 0.680351
13 1.010388 0.005553 0.227647 0.212368
14 3.272408 0.000620 0.846543 0.000149
15 2.354457 0.018608 0.595389 0.774092
16 3.297936 0.017484 0.853528 0.725720
17 2.415297 0.009618 0.612035 0.387285
18 0.439263 0.000617 0.071386 0.000000
19 3.335262 0.005988 0.863740 0.231088
20 2.767412 0.013357 0.708375 0.548171
21 0.830678 0.013824 0.178478 0.568255
22 1.056041 0.007806 0.240138 0.309336
23 1.497400 0.023858 0.360896 1.000000
24 0.629698 0.014088 0.123489 0.579604
25 3.758559 0.020663 0.979556 0.862509
26 0.964214 0.010302 0.215014 0.416719
27 3.680324 0.023647 0.958150 0.990918
28 3.169445 0.017329 0.818372 0.719059
29 1.898905 0.017892 0.470749 0.743299
30 3.322663 0.020508 0.860293 0.855869
31 2.735855 0.010578 0.699741 0.428591
32 2.264645 0.017853 0.570816 0.741636
33 2.613166 0.021359 0.666173 0.892456
34 1.976168 0.001568 0.491888 0.040928
35 3.076169 0.013663 0.792852 0.561335
36 3.330470 0.013048 0.862429 0.534891
37 3.600527 0.012340 0.936318 0.504426
38 0.653994 0.008665 0.130137 0.346288
39 0.587896 0.013134 0.112052 0.538567
40 0.178353 0.011326 0.000000 0.460781
41 3.727127 0.016738 0.970956 0.693658
42 1.719622 0.010939 0.421696 0.444123
43 0.460177 0.021131 0.077108 0.882665
44 3.124722 0.010328 0.806136 0.417826
45 1.011988 0.007631 0.228085 0.301799
46 3.833281 0.003896 1.000000 0.141076
47 3.289872 0.017223 0.851322 0.714495
48 1.906116 0.002058 0.472721 0.062020
49 1.136424 0.022451 0.262131 0.939465