How to estimate the correlation between two functions with unknown variables inside?-CodePudding

I need to solve this optimization problem in order to estimate lambda:

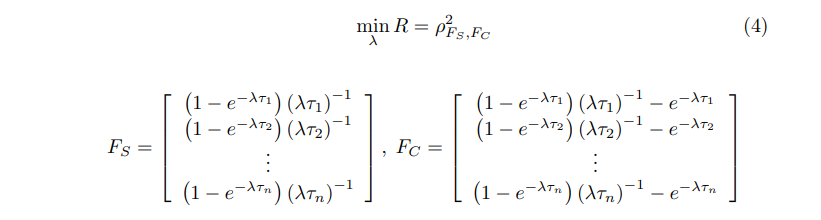
minimization problem

Basically, I need to find the correlation between these two functions:

f1 <- function(lambda, tau){slope = (1-exp(-lambda*tau))/(lambda*tau)            
      return(slope)}

f2 <- function(lambda, tau){curve = ((1-exp(-lambda*tau))/(lambda*tau))-exp(-lambda*tau) 
 return(curve)}

I know the different values of tau. Suppose for example tau = 0.25: now f1 and f2 have only one missing parameter, lambda, which should be estimated. However, when I try to implement the optim() function to be minimized, it does not work since f1 and f2 are not numeric. How can I build this kind of optimization problem mantaining f1 and f2 as functions?

Many thanks

CodePudding user response：

If I am understanding correctly, you are trying to minimise the squared correlation between the output of f1 and f2 at different values of lambda. This means that for each value of lambda you are assessing, you need to feed in the complete vector of tau values. This will give a vector output for each value of lambda so that a correlation between the output from the two functions can be calculated at any single value of lambda.

To do this, we create a vectorized function that takes lambda values and calculates the squared correlation between f1 and f2 at those values of lambda across all values of tau

f3 <- function(lambda) {
  sapply(lambda, function(l) {
      cor(f1(l, seq(1/12, 10, 1/12)), f2(l, seq(1/12, 10, 1/12)))^2
  })
}

To get the optimal value of lambda that minimizes the squared correlation, we just use optimize:

optimize(f3, c(0, 100))$minimum
#> [1] 0.6678021

CodePudding user response：

Perhaps the examples at the bottom of the page help: https://search.r-project.org/CRAN/refmans/NMOF/html/NSf.html

They input a vector of times into the functions (which is fixed for a given yield-curve), so you can compute the correlation for a given lambda. To minimize the correlation, do a grid search over the lambdas. In your case, for instance,

lambda <- 2
cor(f1(lambda, 1:10), f2(lambda, 1:10))

Note that I have assumed maturity measured in years, 1 to 10. You will need to fill in appropriate values. To find a lambda that leads to a low correlation, you could run a grid search.

lambdas <- seq(0.00001, 25, length.out = 1000)
squared.corr <- rep(NA_real_, length(lambdas))

for (i in seq_along(lambdas)) {
    c <- cor(f1(lambdas[i], 1:10),
             f2(lambdas[i], 1:10))
    squared.corr[i] <- c*c
}
lambdas[which.min(c2)]
## [1] 0.490

(I am one of the authors of Gilli, Grosse and Schumann (2010), on which the suggestion to minimize the correlation is based.)