ggeffects: confidence interval for non-linear model-CodePudding

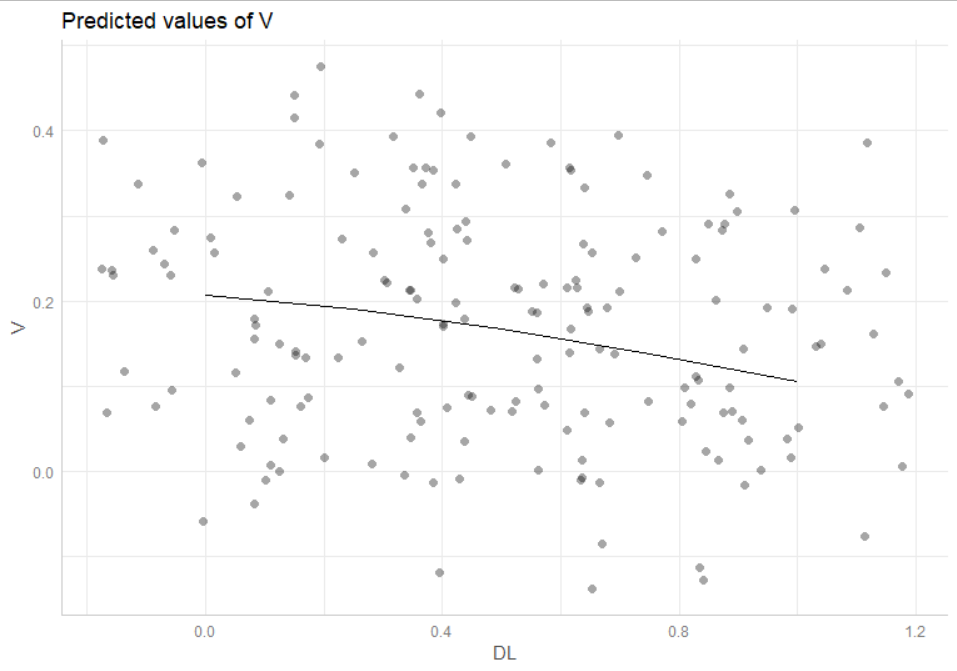
I'd to plot the confidence interval for non-linear models using ggeffects package. In my case:

#Packages
library(ggplot2) 
library(minpack.lm)  
library(ggeffects)
library(dplyr)

# My dataset
coleo<- read.csv("https://raw.githubusercontent.com/Leprechault/PEN-533/master/coleo-infest-tree.csv")
coleo$DL<-as.numeric(coleo$DL)
coleo$V<-as.numeric(coleo$V)

# My model
m.c.coleo<-nlsLM(V ~ b1   b2 * I(DL^b3), start = list(b1 = 0.2164, b2 = 1.6264, b3 = 1), data = coleo)
summary(m.c.coleo)

# My plot
ggpredict(m.c.coleo, terms = "DL [all]") %>% plot(add.data = TRUE)

The output plot doesn't have a confidence interval and normally the package makes it.

Please, any help with it?

CodePudding user response：

I think this is due to the fact that ggpredict uses the generic predict function, and predict.nls does not produce standard errors. From the docs for ggpredict:

ggpredict() uses predict() for generating predictions

And the docs for stats:::predict.nls state:

se.fit A logical value indicating if the standard errors of the predictions should be calculated. Defaults to FALSE. At present this argument is ignored.

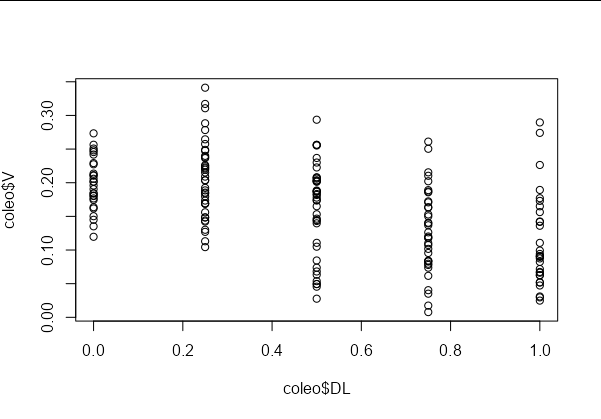
The plot that ggpredict makes for your model seems a bit odd anyway. If you look at the data, there are only 5 discrete values of DL along the x axis:

plot(coleo$DL, coleo$V)

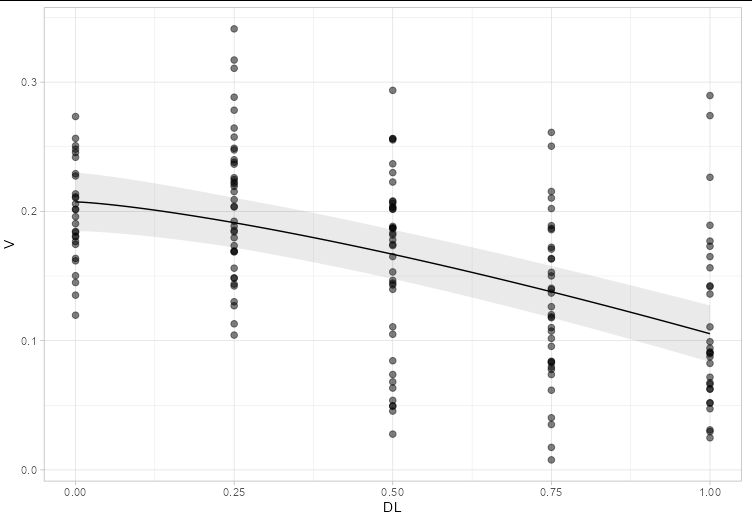
To make a plot which includes the original points, the nls regression line and a confidence interval for the regression line, you could create one yourself in ggplot. The standard error of the mean at each of the discrete values of DL can be approximated by the standard deviation divided by the square root of the number of points at that x value. A smooth band representing the 95% confidence interval can then be constructed by interpolation:

plot_df <- data.frame(
  DL = seq(0, 1, 0.01),
  V = predict(m.c.coleo, newdata = list(DL = seq(0, 1, 0.01))),
  se = 1.96 * summary(m.c.coleo)$sigma / sqrt(approx(sort(unique(coleo$DL)), 
       table(coleo$DL), xout = seq(0, 1, 0.01))$y)
)

ggplot(coleo, aes(DL, V))   
  geom_point(size = 2, alpha = 0.5)  
  theme_light()  
  geom_ribbon(data = plot_df, aes(ymin = V - se, ymax = V   se),
              alpha = 0.1)  
  geom_line(data = plot_df)