Incorrect R lm() slope with plot/interpretation-CodePudding

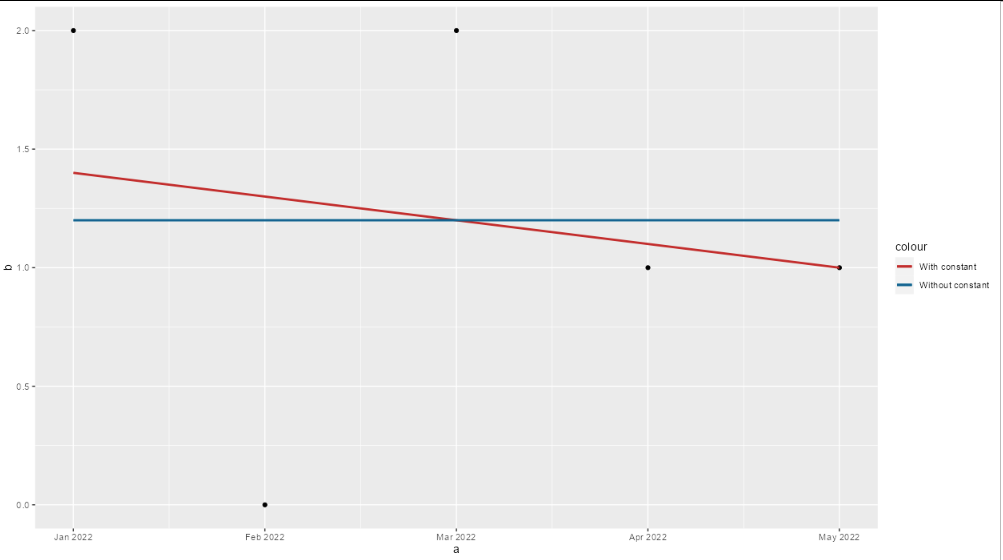
I need a little help understanding the output of my regression model. As a result of lm() I get that my slope is -1.2. However, when plotting the graph, it doesn't looke like the slope is actually -1.2 but much less. I also dont understand why my intercept looks that way. What am I missing?

library(zoo)
library(ggplot2)

a <- as.yearmon(c("2022-01", "2022-02", "2022-03", "2022-04", "2022-05"))
b <- c(2,0,2,1,1)

df <- data.frame(a,b)
df

ggplot(df, aes(x = a, y = b))  
  geom_point()  
  stat_smooth(method = lm)

lm(b ~ a, df)

CodePudding user response：

The plot is fine. unclass(a) shows that the predictor is in years,

unclass(a)
[1] 2022.000 2022.083 2022.167 2022.250 2022.333

The slope is 1.2 per year, and you have a third of a year, so get a change of 0.4.

The intercept is where the predicted value when x = 0. Two thousand and twenty two years to the left of your plot. This is why it is so high

CodePudding user response：

Another way to look at this is to change the units of your time variable so that the regression results match the visual intuition given by the plot. The way to do this is to convert the time variable into "months since first data point":

df$months_since_start <- 12 * (df$a - df$a[1])

df
#>          a b months_since_start
#> 1 Jan 2022 2                  0
#> 2 Feb 2022 0                  1
#> 3 Mar 2022 2                  2
#> 4 Apr 2022 1                  3
#> 5 May 2022 1                  4

Now your lm results are much more in keeping with the plot (an intercept of 1.4 and slope of -0.1 per month)

lm(b ~ months_since_start, df)
#> 
#> Call:
#> lm(formula = b ~ months_since_start, data = df)
#> 
#> Coefficients:
#>        (Intercept)  months_since_start  
#>                1.4                -0.1

I think this is probably a more natural way to present the results, since although it is equivalent numerically, saying that "the value started at 1.4 at the start of the year and has drifted down by 0.1 per month on average" is likely to be more factually accurate than "the value started at 2043 in 1 BCE and has drifted down 1.2 per year since then."

^{Created on 2022-06-21 by the}