Calculating Covariance of datasets-CodePudding

P = np.array(
    [
        [0.03607908, 0.03760034, 0.00503184, 0.0205082 , 0.01051408,
         0.03776221, 0.00131325, 0.03760817, 0.01770659],
        [0.03750162, 0.04317351, 0.03869997, 0.03069872, 0.02176718,
         0.04778769, 0.01021053, 0.00324185, 0.02475319],
        [0.03770951, 0.01053285, 0.01227089, 0.0339596 , 0.02296711,
         0.02187814, 0.01925662, 0.0196836 , 0.01996279],
        [0.02845139, 0.01209429, 0.02450163, 0.00874645, 0.03612603,
         0.02352593, 0.00300314, 0.00103487, 0.04071951],
        [0.00940187, 0.04633153, 0.01094094, 0.00172007, 0.00092633,
         0.02032679, 0.02536328, 0.03552956, 0.01107725]
    ]
)

I have the above dataset where X corresponds to the rows and Y corresponds to the columns. I was wondering how I can find the covariance of X and Y. is it as simple as running np.cov()?

CodePudding user response：

It is as simple as doing np.cov(matrix).

P = np.array(
    [
        [0.03607908, 0.03760034, 0.00503184, 0.0205082 , 0.01051408,
         0.03776221, 0.00131325, 0.03760817, 0.01770659],
        [0.03750162, 0.04317351, 0.03869997, 0.03069872, 0.02176718,
         0.04778769, 0.01021053, 0.00324185, 0.02475319],
        [0.03770951, 0.01053285, 0.01227089, 0.0339596 , 0.02296711,
         0.02187814, 0.01925662, 0.0196836 , 0.01996279],
        [0.02845139, 0.01209429, 0.02450163, 0.00874645, 0.03612603,
         0.02352593, 0.00300314, 0.00103487, 0.04071951],
        [0.00940187, 0.04633153, 0.01094094, 0.00172007, 0.00092633,
         0.02032679, 0.02536328, 0.03552956, 0.01107725]
    ]
)

covariance_matrix = np.cov(P)
print(covariance_matrix)

array([[ 2.24741487e-04,  6.99919604e-05,  2.57114780e-05,
        -2.82152656e-05,  1.06129995e-04],
       [ 6.99919604e-05,  2.26110038e-04,  9.53538651e-07,
         8.16500154e-05, -2.01348493e-05],
       [ 2.57114780e-05,  9.53538651e-07,  7.92448292e-05,
         1.35747682e-05, -8.11832888e-05],
       [-2.82152656e-05,  8.16500154e-05,  1.35747682e-05,
         2.03852891e-04, -1.26682381e-04],
       [ 1.06129995e-04, -2.01348493e-05, -8.11832888e-05,
        -1.26682381e-04,  2.37225703e-04]])

CodePudding user response：

Unfortunately, it is not as simple as running np.cov(); at least in your case.

For the given problem, the table P has only non-negative entries and sums to 1.0. Moreover, since the table is called P and you invoke the random variables X and Y I'm somewhat certain that you present the joint probability table of a discrete, bivariate probability distribution of a random vector (X, Y). In turn, np.cov(X) is not correct as it computes the empirical covariance matrix of a table of datapoints (where each row represents an observation and each column refers to a single feature).

However, you provided the probabilities rather than actual data. This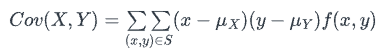

can be efficiently computed via

import numpy as np
# values the random variables can take
X = np.array([0,1,2,3,4])
Y = np.array([0,1,2,3,4,5,6,7,8])

# expectation
mu_X = np.dot(Y, np.sum(P,0))
mu_Y = np.dot(X, np.sum(P,1))

# Covriance by loop
Cov = 0.0
for i in range(P.shape[0]):
    for j in range(P.shape[1]):
        Cov_1  = (X[i] - mu_X)*(Y[j] - mu_Y)*P[i,j]

or, directly via NumPy as

# Covariance by matrix multiplication
mu_X = np.dot(Y, np.sum(P,0))
mu_Y = np.dot(X, np.sum(P,1))
Cov = np.sum(np.multiply(np.outer(X-mu_X, Y-mu_Y), P))

Naturally, both results coincide (up to a floating-point error).

If you replace X and Y with the actual values the random variable can take, yu can simply rerun the code and compute the new covariance value Cov.