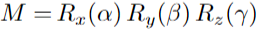Get the smallest Euler angle from a rotation matrix-CodePudding

I have a 3D rotation matrix with small XYZ angles. Angles are between -20° < angle < 20°.
Rotation matrix is constructed with :

I want to get angles back from the rotation matrix, but several angles are possible.

How to recover the smallest angles allowing to build this rotation matrix in C ?

For the moment I use Eigen::eulerAngles() in C to get this angles, but Eigen return angle in the ranges x[0:pi] y[-pi:pi] z[-pi:pi]. So no negative X angles are returned. We can see that a rotation matrix constructed with a X angle of -0.2 return an angle of 2.94159

Here is a test code:

void eigen_test(float x, float y, float z) {
  auto mat = AngleAxisf(x, Vector3f::UnitX())
    * AngleAxisf(y, Vector3f::UnitY())
    * AngleAxisf(z, Vector3f::UnitZ());

  auto angle = mat.toRotationMatrix().eulerAngles(0,1,2);

  cout << "(" <<  x << ", " << y << ", " << z << ") 
-> (" << angle[2] << ", " << angle[1] << ", " << angle[0] << ")" << endl;

}

int main() {
  std::vector<float> num = { -0.2,0.,0.2 };
  for (auto x : num) {
    for (auto y : num) {
      for (auto z : num) {
        eigen_test(x, y, z);
      }
    }
  }

  return 0;
}

Full result :

X    , Y   , Z     -> X'   , Y'   , Z'
__________________________________________________
(-0.2, -0.2, -0.2) -> (2.94159, -2.94159, 2.94159)
(-0.2, -0.2, 0   ) -> (2.94159, -2.94159, -3.14159)
(-0.2, -0.2, 0.2 ) -> (2.94159, -2.94159, -2.94159)
(-0.2, 0,    -0.2) -> (2.94159, -3.14159, 2.94159)
(-0.2, 0,    0   ) -> (2.94159, 3.14159, -3.14159)
(-0.2, 0,    0.2 ) -> (2.94159, 3.14159, -2.94159)
(-0.2, 0.2,  -0.2) -> (2.94159, 2.94159, 2.94159)
(-0.2, 0.2,  0   ) -> (2.94159, 2.94159, 3.14159)
(-0.2, 0.2,  0.2 ) -> (2.94159, 2.94159, -2.94159)
(0,   -0.2,  -0.2) -> (0, -0.2, -0.2)
(0,   -0.2,  0   ) -> (0, -0.2, 0)
(0,   -0.2,  0.2 ) -> (3.14159, -2.94159, -2.94159)
(0,   0,     -0.2) -> (0, 0, -0.2)
(0,   0,     0   ) -> (-0, 0, -0)
(0,   0,     0.2 ) -> (-0, 0, 0.2)
(0,   0.2,   -0.2) -> (3.14159, 2.94159, 2.94159)
(0,   0.2,   0   ) -> (-0, 0.2, 0)
(0,   0.2,   0.2 ) -> (0, 0.2, 0.2)
(0.2, -0.2,  -0.2) -> (0.2, -0.2, -0.2)
(0.2, -0.2,  0   ) -> (0.2, -0.2, -0)
(0.2, -0.2,  0.2 ) -> (0.2, -0.2, 0.2)
(0.2, 0,     -0.2) -> (0.2, 0, -0.2)
(0.2, 0,     0   ) -> (0.2, 0, 0)
(0.2, 0,     0.2 ) -> (0.2, 0, 0.2)
(0.2, 0.2,   -0.2) -> (0.2, 0.2, -0.2)
(0.2, 0.2,   0   ) -> (0.2, 0.2, -0)
(0.2, 0.2,   0.2 ) -> (0.2, 0.2, 0.2)

CodePudding user response：

I have found how to do for angles between pi/2 and -pi/2 (so work with small angles).
For a rotation ordering of xyz, you can do:

//mat is the 3*3 rotation matrix
double rx = atan2(-mat(1, 2), mat(2, 2));
double ry = asin(mat(0, 2));
double rz = atan2(-mat(0, 1), mat(0, 0));

Found more info on https://www.geometrictools.com/Documentation/EulerAngles.pdf