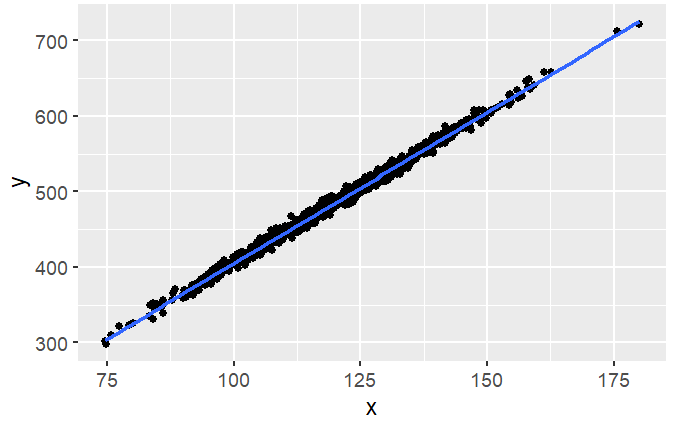
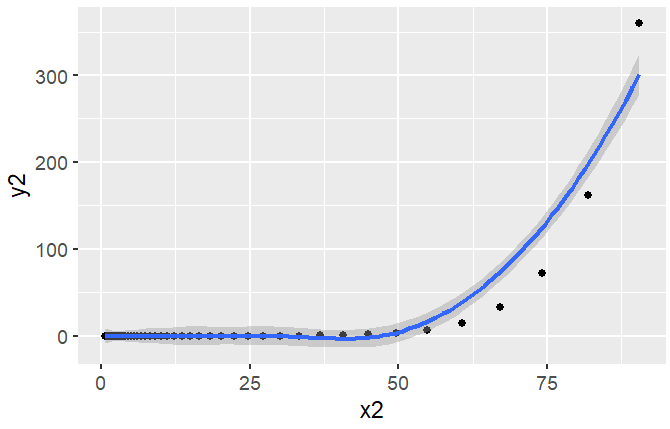
I have created a normal bivariate dataset with a strong linear association below:

#### Load Library ####
library(tidyverse)

#### Create Data ####
x <- rnorm(n=1000, mean=120, sd=15)
y <- 4*x   5   rnorm(n=1000, mean = 0, sd = 5)
df <- data.frame(x,y)

#### Plot ####
ggplot(df,
       aes(x,y)) 
  geom_point() 
  geom_smooth(method = "lm")

#### Run Regression ####
lm.xy <- lm(y~x,
            data = df)
summary(lm.xy)

Which gives me what I want, a linear relationship and a model that fits (the R2 is understandably above 90%):

I have tried to do the same thing with exponential data like so:

#### Create Exponential Data ####
x2 <- dexp(1:50, rate=.1)*1000
y2 <- dexp(1:50, rate=.8)*1000
df2 <- data.frame(x2,y2)

#### Plot ####
ggplot(df2,
       aes(x=x2,
           y=y2)) 
  geom_point() 
  geom_smooth()

Plotting this, there is no issue:

However, I'm not sure how to model this with a regression. If I do the typical regression formula:

#### Run Regression ####
exp.reg <- lm(y2 ~ x2,
              df2)
summary(exp.reg)

It will understandably have a much less precise model:

Residual standard error: 42.66 on 48 degrees of freedom
Multiple R-squared:  0.4305,    Adjusted R-squared:  0.4187 
F-statistic: 36.29 on 1 and 48 DF,  p-value: 2.302e-07

Additionally, I tried labeling the regression equation to the plot:

ggplot(df2,
       aes(x=x2,
           y=y2)) 
  geom_point() 
  geom_smooth() 
  stat_regline_equation(aes(exp.reg))

But this gave me an error:

Error in `check_aesthetics()`:
! Aesthetics must be either length 1 or the same as the data (50): x

So my question has two parts. First, how do I model an exponential regression properly? Second, how do I annotate that regression equation onto ggplot?

CodePudding user response：

A few comments:

1. In your exponential data example, geom_smooth without additional arguments fits a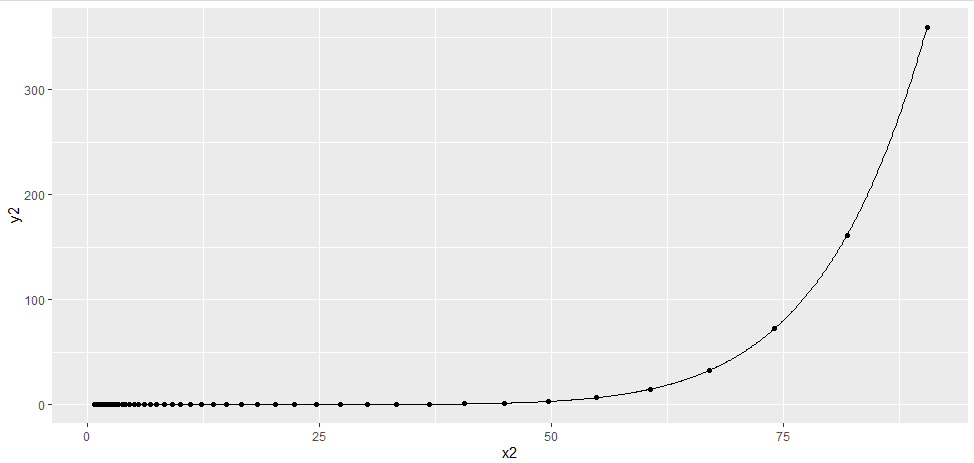

   The coefficients of fit are

   summary(fit)$coefficients
   #             Estimate   Std. Error       t value Pr(>|t|)
   #(Intercept) -30.15675 7.152374e-16 -4.216327e 16        0
   #log(x2)       8.00000 2.848167e-16  2.808824e 16        0
   #Warning message:
   #    In summary.lm(fit) : essentially perfect fit: summary may be unreliable
   

   Note the warning which is due to the way that you generated data from dexp (without any errors).

   Also note the slope estimate (on the log scale) of 8.0, which is just the ratio of your two dexp rate parameters 0.8/0.1.