I've been tasked to correct for saturation in our photon detector. The data should be increasing linearly, however after a certain value (~5000) the counts begin to saturate.

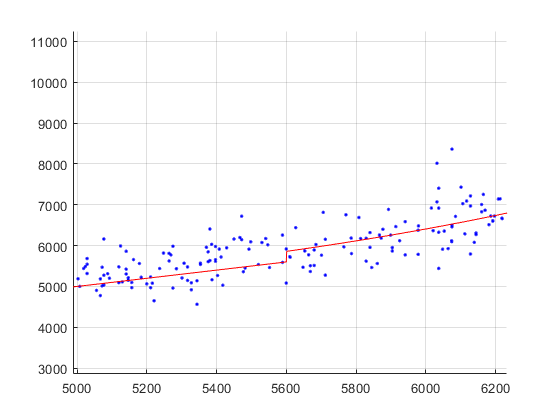
To measure this we then took a series of measurements of the same sample at different laser powers. Presuming the linear trend would continue we can predict what the values should be if the linear trend had continued. This is shown in the plot below (x-axis = actual values obtained, y-axis = predicted values, blue dots = sample values).

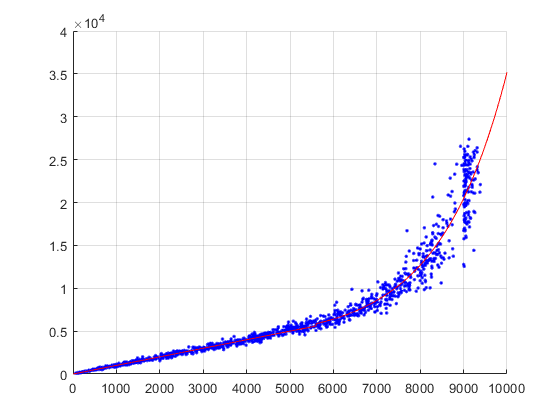
I then used nlinfit in MATLAB to try to fit the equation linearly at values below a threshold and exponentially above the threshold.

modelfun= @(b,x) ((x<b(1)).*x(:,1))   ((x>b(1)).*((b(2).*exp(b(3).*x)) b(4)));
beta0=[5000,1,0.001,100];
beta=nlinfit(TrueValues,PredictedValues,modelfun,beta0);

I then plotted the result(red line). Which seems to fit really nicely

But if I zoomed into the part where the transition from linear to exponential occurs there is a small step of approximately 200

I've tried to minimise this step size but there is no way to completely get rid of it.

Does anyone have any suggestions? Especially if there is a more elegant equation that can transition from linear to exponential. Happy for the suggestions to be in MATLAB, Python or R. Thanks in advance!

CodePudding user response：

Without data I will not be able to check if this works (in the sense, will the fit be good enough for you on the non linear part). But it will definitely be continuous, because the continuity will be embedded in the system (the transition point between your two sections will have coordinates [b(1) b(1)]).

You can add this constraint by removing the 4th constant b(4) and replacing it by

b(1) - ((b(2).*exp(b(3).*b(1))).

modelfun= @(b,x) ((x<=b(1)).*x(:,1))   ((x>b(1)).*((b(2).*exp(b(3).*x)) b(1)-((b(2).*exp(b(3).*b(1)))));
beta0=[5000,1,0.001];
beta=nlinfit(TrueValues,PredictedValues,modelfun,beta0);

CodePudding user response：

An alternative to the other models mentioned would be removing this discontinuity by using a smooth approximation to your step/indicator function, so for instance by approximating (x > c) with sigmoid(x - c) where

sigmoid = @(x) 1 ./(1 exp(-x));

(and similarly (x <= c) with 1-sigmoid(x-c)).

Ideally you'd also introduce a scaling parameter (i.e. a b(5)) to scale it horizontally as

sigmoid = @(x, sc) 1./(1 exp(-sc*x));

CodePudding user response：

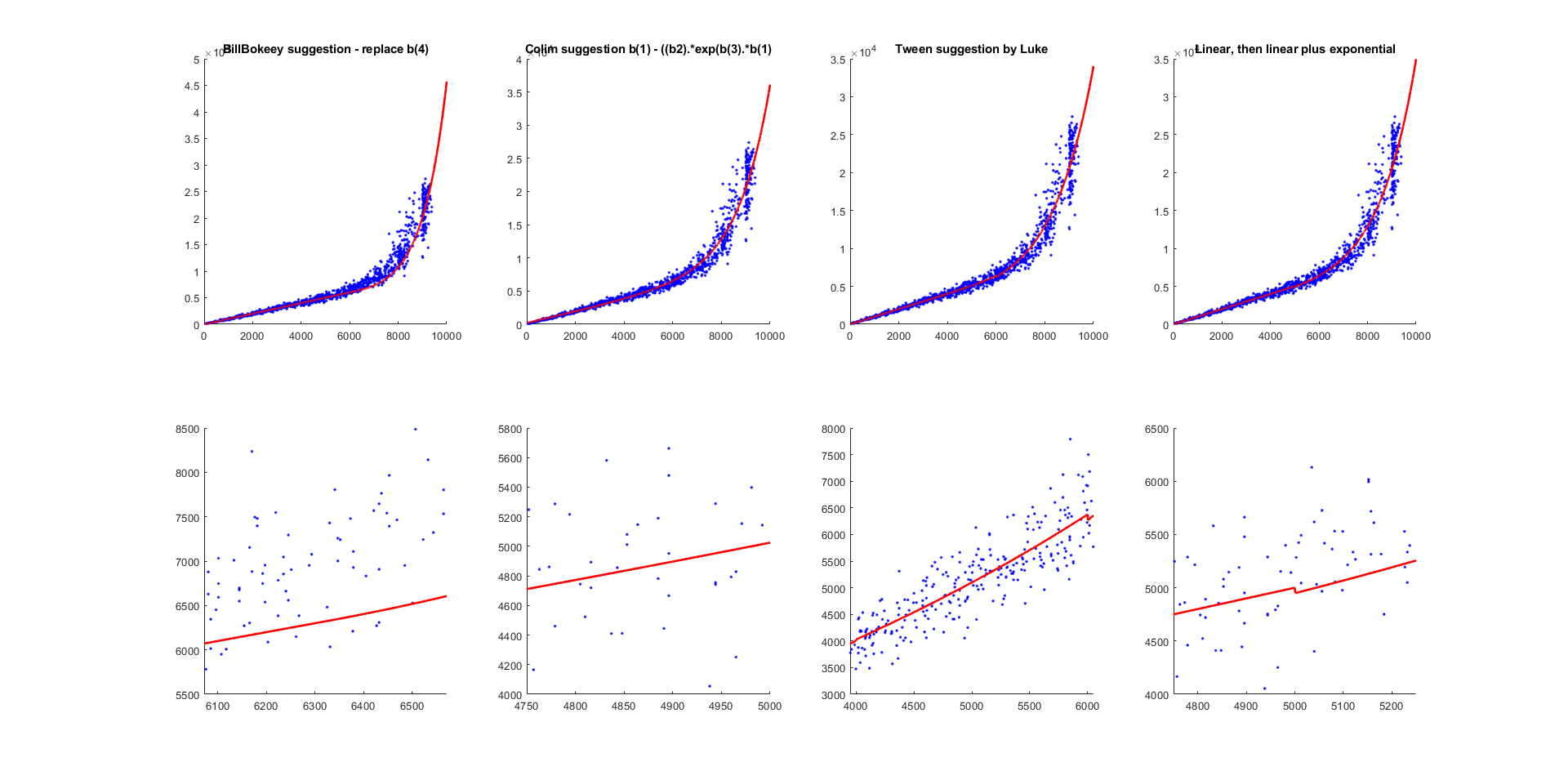
Don't know if it's appropriate to place this all as an answer, but I've tried all the options except for @flawr's.

The tldr is that @Colim's answer (b0 b1*x b2*e^(b3*x)) in the comment provides the best fit...

The figure above shows the 4 different options that I've tried including one where I tried to model an exponential on top of a linear above a particular threshold value (right panel). The bottom row serves as insets to look for steps.

The slightly longer answer is that only @BillBokeey's answer and @Colim's don't have a step. But Colim's suggestion seems to fit the data better in the exponential range.

As a Caveat @Luke's suggestion would probably work if you added different weightings that change as your x value increases. Perhaps even with sigmoidal weights which may be what @flawr is suggesting. Additionally, the steps are really small so it could probably work in the future for anyone trying to combine two different equations into one.