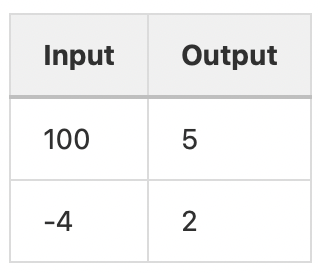
I have some task:

You can use basic control structures–sequence, branch, loop, as well as addition, subtraction, and multiplication. You cannot use division: this module is designed to run on microcontrollers. Create an src/1948.c file which takes a number into stdin after compilation and launch, and calculates its largest prime divisor.

Is there any way to find the largest prime divisor of any predetermined integer without using division and the operation of taking the remainder of the division?

CodePudding user response：

Of course you could just write a division function and then call that to do division.

Alternatively, you can write a square root function and use (a b)(a-b) = a² - b². After removing the factors of 2, start with the smallest a >= sqrt(N), and then check every a² - N to see if it's square.

CodePudding user response：

A nested loop would not be efficient but it would find the factor eventually:

static int get_largest_factor(int n)
{
    if ((n == 0) || (n*n == 1))
    {
        return n;
    }
    else if (n < 0)
    {
        //  recursion to avoid negatives
        return get_largest_factor(-n);
    }
    else
    {
        int fMax = 1;

        //  try all non-trivial factors
        //  up to sqrt(n)
        for (int f = 2; f*f <= n; f  )
        {
            //  repeat add to avoid division
            for (int p = f; p < n 1; p  = f)
            {
                if (p == n)
                {
                    //  new factor found
                    fMax = f;
                    break;
                }
            }
        }

        return (fMax == 1) ? n : fMax;
    }
}

CodePudding user response：

By the Sieve of Eratosthenes

Suppose the predetermined integer is N.
Store N as the 'highest prime divisor'.
Allocate an array with (N >> 1) 1 elements and fill with 0.

Start with the first prime 2.
Check off every multiple of the prime in the array (with an addition loop).
Continue finding multiples right up to N.
If it hits N exactly, store this prime as the 'highest prime divisor'.
Find the next prime.
This will be the next unchecked element in the sieve - the array.
But if you've passed the end of the array then you are done.
Otherwise repeat as you did for the previous prime.