I have two uint16 3D (GPU) arrays A and B in MATLAB, which have the same 2nd and 3rd dimension. For instance, size(A,1) = 300 000, size(B,1) = 2000, size(A,2) = size(B,2) = 20, and size(A,3) = size(B,3) = 100, to give an idea about the orders of magnitude. Actually, size(A,3) = size(B,3) is very big, say ~ 1 000 000, but the arrays are stored externally in small pieces cut along the 3rd dimension. The point is that there is a very long loop along the 3rd dimension (cfg. MWE below), so the code inside of it needs to be optimized further (if possible). Furthermore, the values of A and B can be assumed to be bounded way below 65535, but there are still hundreds of different values.

For each i,j, and d, the rows A(i,:,d) and B(j,:,d) represent multisets of the same size, and I need to find the size of the largest common submultiset (multisubset?) of the two, i.e. the size of their intersection as multisets. Moreover, the rows of B can be assumed sorted.

For example, if [2 3 2 1 4 5 5 5 6 7] and [1 2 2 3 5 5 7 8 9 11] are two such multisets, respectively, then their multiset intersection is [1 2 2 3 5 5 7], which has the size 7 (7 elements as a multiset).

I am currently using the following routine to do this:

s = 300000; % 1st dim. of A
n = 2000; % 1st dim. of B
c = 10; % 2nd dim. of A and B
depth = 10; % 3rd dim. of A and B (corresponds to a batch of size 10 of A and B along the 3rd dim.)
N = 100; % upper bound on the possible values of A and B

A = randi(N,s,c,depth,'uint16','gpuArray');
B = randi(N,n,c,depth,'uint16','gpuArray');

Sizes_of_multiset_intersections = zeros(s,n,depth,'uint8'); % too big to fit in GPU memory together with A and B
for d=1:depth
    A_slice = A(:,:,d);
    B_slice = B(:,:,d);
    unique_B_values = permute(unique(B_slice),[3 2 1]); % B is smaller than A

    % compute counts of the unique B-values for each multiset:
    A_values_counts = permute(sum(uint8(A_slice==unique_B_values),2,'native'),[1 3 2]);
    B_values_counts = permute(sum(uint8(B_slice==unique_B_values),2,'native'),[1 3 2]);

    % compute the count of each unique B-value in the intersection:
    Sizes_of_multiset_intersections_tmp = gpuArray.zeros(s,n,'uint8');
    for i=1:n
        Sizes_of_multiset_intersections_tmp(:,i) = sum(min(A_values_counts,B_values_counts(i,:)),2,'native');
    end

    Sizes_of_multiset_intersections(:,:,d) = gather(Sizes_of_multiset_intersections_tmp);
end

One can also easily adapt above code to compute the result in batches along dimension 3 rather than d=1:depth (=batch of size 1), though at the expense of even bigger unique_B_values vector.

Since the depth dimension is large (even when working in batches along it), I am interested in faster alternatives to the code inside the outer loop. So my question is this: is there a faster (e.g. better vectorized) way to compute sizes of intersections of multisets of equal size?

CodePudding user response：

Disclaimer : This is not a GPU based solution (Don't have a good GPU). I find the results interesting and want to share, but I can delete this answer if you think it should be.

Below is a vectorized version of your code, that makes it possible to get rid of the inner loop, at the cost of having to deal with a bigger array, that might be too big to fit in the memory.

The idea is to have the matrices A_values_counts and B_values_counts be 3D matrices shaped in such a way that calling min(A_values_counts,B_values_counts) will calculate everything in one go due to implicit expansion. In the background it will create a big array of size s x n x length(unique_B_values) (Probably most of the time too big)

In order to go around the constraint on the size, the results are calculated in batches along the n dimension, i.e. the first dimension of B:

tic

nBatches_B = 2000;
sBatches_B = n/nBatches_B;
Sizes_of_multiset_intersections_new = zeros(s,n,depth,'uint8');

for d=1:depth
    A_slice = A(:,:,d);
    B_slice = B(:,:,d);

    % compute counts of the unique B-values for each multiset:    
    unique_B_values = reshape(unique(B_slice),1,1,[]);

    A_values_counts = sum(uint8(A_slice==unique_B_values),2,'native'); % s x 1 x length(uniqueB) array
    B_values_counts = reshape(sum(uint8(B_slice==unique_B_values),2,'native'),1,n,[]); % 1 x n x length(uniqueB) array

    % Not possible to do it all in one go, must split in batches along B

    for ii = 1:nBatches_B

        Sizes_of_multiset_intersections_new(:,((ii-1)*sBatches_B 1):ii*sBatches_B,d) = sum(min(A_values_counts,B_values_counts(:,((ii-1)*sBatches_B 1):ii*sBatches_B,:)),3,'native'); % Vectorized
    
    end

end

toc

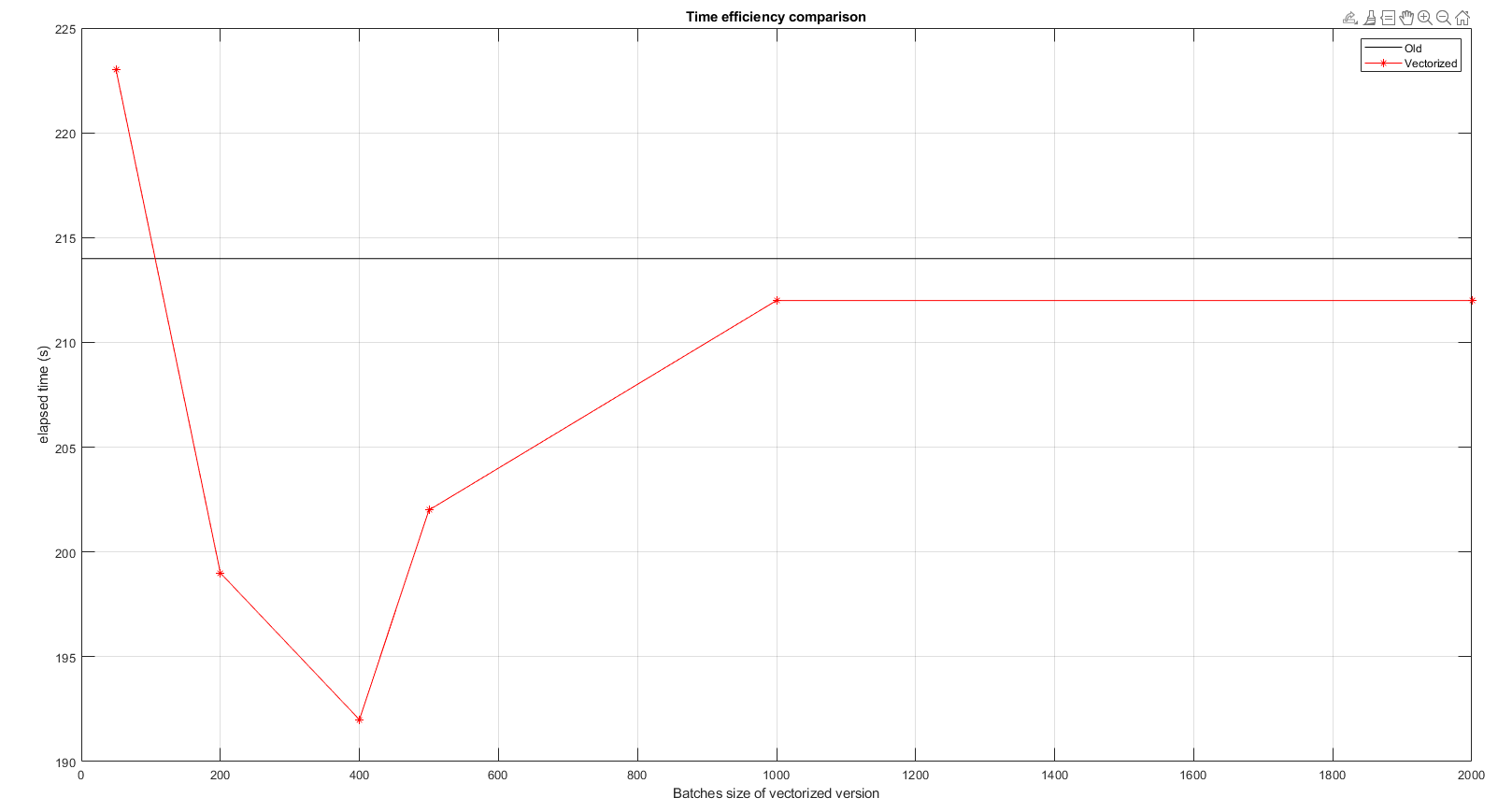
Here is a little benchmark with different values of the number of batches. You can see that a minimum is found around a number of 400 (batch size 50), with a decrease of around 10% in processing time (each point is an average over 3 runs). (EDIT : x axis is amount of batches, not batches size)

I'd be interested in knowing how it behaves for GPU arrays as well!