Sklearn KNeighborsClassifier gives different results when using KNeighborsTransformer?-CodePudding

I am trying to get my head around how to use KNeighborsTransformer correctly, so I am using the Iris dataset to test it. However, I find that when I use KNeighborsTransformer before the KNeighborsClassifier I get different results than using KNeighborsClassifier directly.

When I plot the decision boundaries, they are similar, but different.

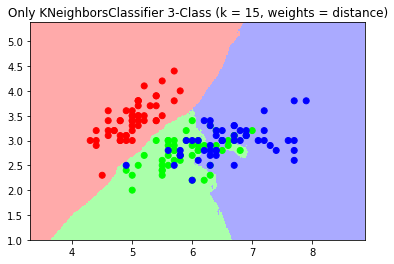
I have given the metric and weights mode explicitly, so that cannot be the problem.

Why do I get this difference? Does it have something to do with whether they count a point as its own nearest neighbour? Or does it have something to do with the metric='precomputed'?

Below is the code I use to consider the two classifiers.

import numpy as np
from sklearn import neighbors, datasets
from sklearn.pipeline import make_pipeline


# import data 
iris = datasets.load_iris()

# We only take the first two features. 
X = iris.data[:, :2]
y = iris.target

n_neighbors = 15

knn_metric = 'minkowski'
knn_mode = 'distance'

# With estimator with KNeighborsTransformer
estimator = make_pipeline(
    neighbors.KNeighborsTransformer(
        n_neighbors = n_neighbors   1, # one extra neighbor should already be computed when mode == 'distance'. But also the extra neighbour should be filtered by the following KNeighborsClassifier
        metric = knn_metric,
        mode = knn_mode),
    neighbors.KNeighborsClassifier(
        n_neighbors=n_neighbors, metric='precomputed'))

estimator.fit(X, y)
print(estimator.score(X, y)) # 0.82


# with just KNeighborsClassifier

clf = neighbors.KNeighborsClassifier(
    n_neighbors, 
    weights = knn_mode,
    metric = knn_metric)
clf.fit(X, y)
print(clf.score(X, y)) # 0.9266666666666666

CodePudding user response：

Your pipeline approach uses the default uniform vote, but your direct approach uses the distance-weighted vote. Making them match (either both distance or both uniform) almost makes the behavior match; the seeming remaining difference is in tie-breaking of nearest neighbors; I'm not sure yet why the tie-breaking is happening differently in the two cases, but it's likely not such a big issue with more realistic datasets.