I have a 3D geometry problem and I am not certain of the best approach to solve it. I have a model with two boxes, one above the others. They have the same dimension, L (length) * p (depth) * e (thickness), and are separated by a height of h. They are perfectly superposed, with no offset between them.
For each point of my bottom box, I want to get the zenith of all lines that can cross the top box and arrive to this point. It doesn't matter if the line crosses the top box by the top or the side.
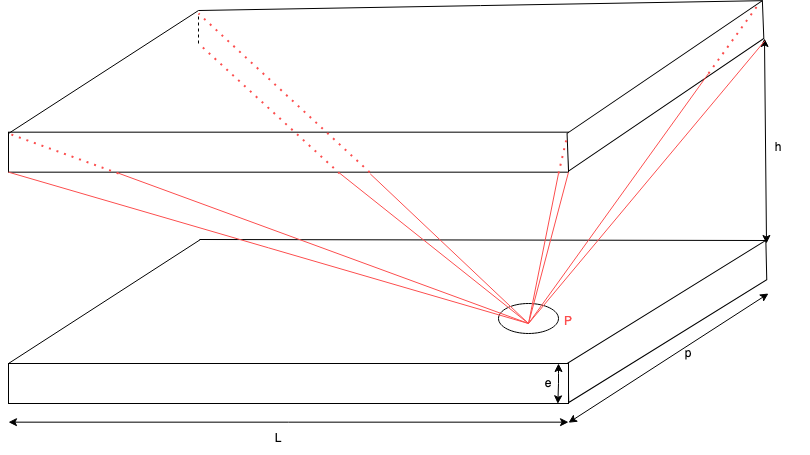
The zenith is the angle of "looking up". In our case, a zenith of 0 represents the point directly above the point P, and an angle of 90 is directly looking in front. A zenith of 180 would be looking below the point, but for our use, it's useless. The zeniths we look for are between 0 and 90°.
For a more intuitive visualization, let's say that I have a hole in the ceiling, and that I want to map the zenith of all light that crosses this hole and reaches the floor.
This is what it looks like:
For any point P of the bottom box, I want an array containing the zeniths of all "rays" that cross the top box before arriving on P. The red lines are the "edges", the last zeniths I would get for each corner.
I am working on a way to code it in MATLAB and I was wondering if there was a better algorithm that I am not seeing. My approach, in pseudocode, would be this:
bottomBox = [1:L, 1:p, 1:e];
topBox = [1:L, 1:p, 1 h:e h];
results = zeros(L:p) * NaN; % Array of results, one per "case" on the bottom box
zeniths = zeros(L:p) * NaN; % Array of zeniths for each result case
for i = 1:L
for j = 1:p % Browsing the bottom box case by case
for k = 1:L
for l = 1:p
for m = 1:e % For each bottom box case, browsing the top box case by case
p1 = topBox(k,l,m); % p1 is each case on the top box
p2 = bottomBox(i,j,1); % p2 is the current bottom box case, z doesn't mattter
p3 = topBox(i,j,m); % p3 is the projection of p2 on the top box (zenith = 0)
v1 = p1 - p2;
v2 = p3 - p2;
zeniths(k,l) = rad2deg(atan2(norm(cross(p1, p2)), dot(p1, p2)));
end
end
end
results(i,j) = zeniths;
end
end
I tried to implement this and I couldn't get it to work. More specifically, the angle calculation doesn't seem to work, I have an error stating:
Error using cross; A and B must be of length 3 in the dimension in which the cross product is taken.
I am looking for advice on how to build the algorithm.
Please tell me if the question is better suited for another StackExchange community, such as Math.
CodePudding user response:
Zenith angle is just
atan2(h, sqrt(dx^2 dy^2))
where dx, dy are coordinate differences along L and p axes (i-k and j-l in your loops)
Perhaps h m (m as your variable for m = 1:e) instead of h if you need points inside top box
CodePudding user response:
I'll get you started showing you one way to do it for 1 point and I'll let you build the final loop to do the calc for all your points.
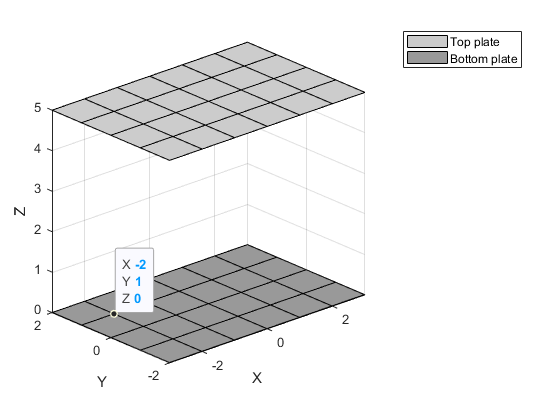
As expressed in the comment, for the purpose of these calculations, you do not need to consider the thickness of your plates, you can model them simply with two parallel planes separated by a distance H.
I don't know the size of your plates nor the grid size you want so I'll keep it simple for this example:
H = 5 ; % distance between the planes
[X,Y] = meshgrid(-3:3,-2:2) ;
GridSize = size(X) ;
Zb = zeros(GridSize) ;
Zt = zeros(GridSize) H ;
This gives you 4 matrices, defining 2 planes. The bottom plane is composed of [X,Y,Zb] and the top plane is formed by [X,Y,Zt].
If you want to visualise them, you can run the following code (optional):
%% Display planes
figure ;
ht = surf(X,Y,Zt, 'FaceColor',[.8 .8 .8],'DisplayName','Top plate') ;
hold on
hb = surf(X,Y,Zb, 'FaceColor',[.6 .6 .6],'DisplayName','Bottom plate') ;
xlabel('X') ; ylabel('Y') ; zlabel('Z') ;
axis equal ; legend show
Now for the rest of the example, I selected a point P, at coordinate [-2,1,0]. This choice is completely arbitrary, just for the example. In your final algorythm you will still have to loop over several points Pi (although remember that your problem is symetric so if your domain is too large you can reduce your computations by using the symetries of your model).
%% This will have to be embedded into a loop over the points Pi
% Assuming points P=(-2,1,0)
p = [-2;1;0] ;
zn = [0;0;1] ; % unitary vector, oriented Oz
dx = X - p(1) ; % `x` distance between all points of the plane and P
dy = Y - p(2) ; % `y` distance between all points of the plane and P
dz = zeros(size(X)) H ; % `z` distance (all the same)
V = [dx(:) dy(:) dz(:)].' ; % to obtain list of vector V = [dx;dy;dz] ;
nv = size(V,2) ; % number of points/angle to calculate
zenith = zeros(nv,1) ; % preallocate result matrix (always good!)
for k=1:nv
% [u] is the vector going from `P` to the current point considered on the top plane
u = V(:,k) ;
% determine the angle between [u] and [zn]
zenith(k) = atan2( norm(cross(u,zn)) , dot(u,zn) ) ;
end
% Reshape "zenith" from vector to matrix so it matches the base grid system
zenith = reshape( zenith , GridSize ) ;
You now have, for this point P, a matrix of angle with every other point of the top plane:
>> rad2deg(zenith)
ans =
32.31 30.96 32.31 35.80 40.32 45.00 49.39
24.09 21.80 24.09 29.50 35.80 41.81 47.12
15.79 11.31 15.79 24.09 32.31 39.51 45.56
11.31 0 11.31 21.80 30.96 38.66 45.00
15.79 11.31 15.79 24.09 32.31 39.51 45.56
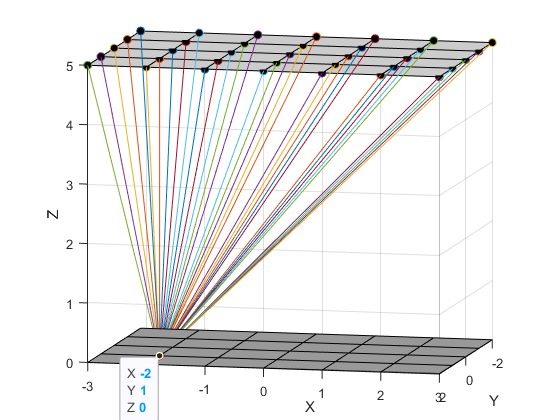
Once again, completely optionally, if you want to visualise the vectors which were used for the calculations:
for k=1:nv
hp(k) = plot3([p(1) X(k)],[p(2) Y(k)],[0 H],'Marker','o','MarkerFaceColor','k') ;
end
will yield:
Now for your final result, remember you have a 2D matrix for each point P of your bottom plane, so your final result will either be a collection of 2D matrices or a large 3D matrix.