Two plots with different x ranges on the same figure, with sympy-CodePudding

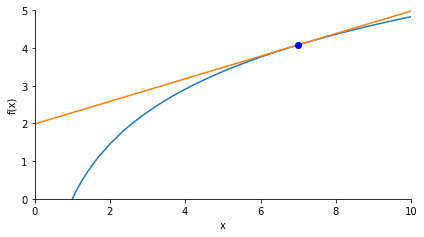
I'm plotting the curve of a function, and it's tangent at point p. I would like to manage xlim for the curve and the tangent independently. In this code the tangent half-length should be 1:

from sympy import init_printing, symbols, N, plot
from sympy import diff
from sympy import log, cos, atan

init_printing()
x = symbols('x')

# Plot a tangent at point (p_x, p_y), of length l
def plot_line(p_x, p_y, x, a, l):
    # Compute b, build tangent expression
    b = p_y - a*p_x
    t = a*x   b
    
    # Limit line length
    r = atan(a) # angle in rad
    dx = N(l*cos(r)) # half range for x
    lims = {'xlim': (p_x-dx, p_x dx)}
    
    # Build plot
    t_plot = plot(t, show=False, **lims)
    return t_plot

# Function
y = 2.1*log(x)

# Point
px = 7
py = y.subs(x, px)

# Plot curve and point
marker = {'args': [px, py, 'bo']}
lims = {'xlim': (0,10), 'ylim': (0,5)}
plots = plot(y, markers=[marker], show=False, **lims)

# Find derivative, plot tangent
y_d = diff(y)
a = y_d.subs(x, px)
plots.extend(plot_line(px, py, x, a, 1))

# Finalize and show plots
plots.aspect_ratio=(1,1)
plots.show()

However this is not the case...

CodePudding user response：

SymPy's plot() function signature is something similar to this:

plot(expr, range, **kwargs)

where range is a 3-elements tuple: (symbol, min_val, max_val). The plot function will evaluate expr starting from min_val up to max_val.

One of the **kwargs is xlim, which is a 2-element tuple: xlim=(x_min, x_max). It is used to restrict the visualization along the x-axis from x_min to x_max. Nonetheless, the numerical values computed by the plot function go from min_val to max_val.

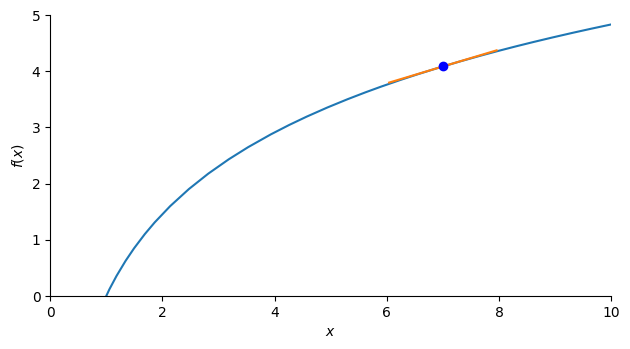
With that said, you need to remove xlim from inside plot_line and provide the range argument instead:

from sympy import init_printing, symbols, N, plot
from sympy import diff
from sympy import log, cos, atan

init_printing()
x = symbols('x')

# Plot a tangent at point (p_x, p_y), of length l
def plot_line(p_x, p_y, x, a, l):
    # Compute b, build tangent expression
    b = p_y - a*p_x
    t = a*x   b
    
    # Limit line length
    r = atan(a) # angle in rad
    dx = N(l*cos(r)) # half range for x
    
    # Build plot
    # Need to provide the range to limit the line length
    t_plot = plot(t, (x, p_x-dx, p_x dx), show=False)
    return t_plot

# Function
y = 2.1*log(x)

# Point
px = 7
py = y.subs(x, px)

# Plot curve and point
marker = {'args': [px, py, 'bo']}
lims = {'xlim': (0,10), 'ylim': (0,5)}
plots = plot(y, markers=[marker], show=False, **lims)

# Find derivative, plot tangent
y_d = diff(y)
a = y_d.subs(x, px)
plots.extend(plot_line(px, py, x, a, 1))

# Finalize and show plots
plots.aspect_ratio=(1,1)
plots.show()